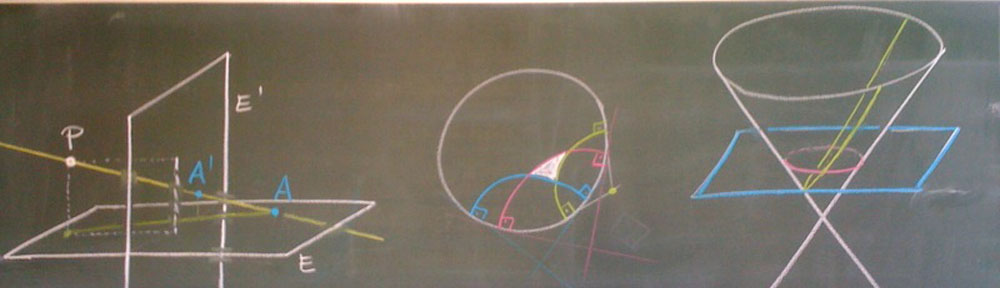Cross-ratio of lines through a point (again).
Claim. The map which maps a point $g^{\ast} \in p^{\ast}$ to the intersection point of $g \cap \ell$ is a projective map.
Proof.
Let $\{b_1,b_2,b_3\}$ be a basis of $\mathbb{R}^3$, such that $P = [b_1]$ and $\ell =P(\text{span} \{b_2,b_3\} )$. This yields a dual basis $\{b_1^{\ast},b_2^{\ast},b_3^{\ast}\}$ of $\mathbb{R}^3$ with $b_i^{\ast}(b_j) = \delta_{i j}$. The line in $(\RP^2)^\ast$ corresponding to the point $P$ is $P^{\ast} = P( \{b_1\}^\circ ) = P(\text{span} \{b_2^\ast,b_3^\ast\} )$.
Let $g^{\ast} = [s b_2^{\ast}+t b_3^{\ast}] \in p^{\ast}$ be a point on the line $P^\ast$. A point $x \in\ell$ can be written as $Q = [x b_2 + y b_3]$. To have $Q \in g $, we need
\[
0 = (s b_2^{\ast} +t b_3^{\ast} )(x b_2 + y b_3) = s x + t y\,.
\]
Solving this for $x$ and $y$ yields the following point of intersection $Q = g {\cap}\ell = [- t b_2 + s b_3]$, so the map $P^\ast \to\ell$ is given by
\[
g \cap\ell =
\left[
\begin{pmatrix}
0 & -1\\
1 & 0
\end{pmatrix}
\begin{pmatrix}
s \\
t
\end{pmatrix}
\right]
\]
for $g = [s b_2^{\ast} + t b_3^{\ast}]$.
Hence, it is a projective transformation and preserves cross-ratio.
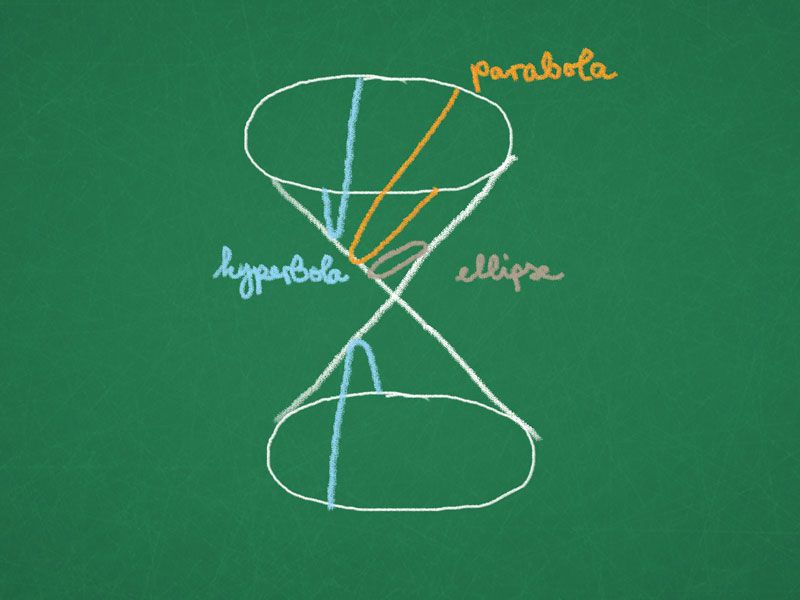
Conic Sections (Euclidean Point of View)
Conic sections are solution sets of the following quadratic equations
\begin{align*}
\left\{ \rvector{u\\v} \in \R^2 | a u^2 + 2 b u v + c v^2 + d u + e v + f = 0 \right\}\,.
\end{align*}
Theorem. Any quadratic equation in Euclidean coordinates can be transformed by an Euclidean motion $\svector{x\\y} = A \svector{u\\v} + b$, with $A\in O(2,\mathbb{R}), b \in \mathbb{R}^2$ to one of the following forms:
- $(\frac{x}{a})^2 + (\frac{y}{b})^2 = 1$, ellipse
- $(\frac{x}{a})^2 – (\frac{y}{b})^2 = 1$, hyperbola
- $y = a x^2$, parabola
- $(\frac{x}{a})^2 – (\frac{y}{b})^2 = 0$, pair of crossing lines
- $x^2 = a^2$, two parallel lines

- $x^2 = 0$, a double line
- $(\frac{x}{a})^2 + (\frac{y}{b})^2 = 0$, a point
- $(\frac{x}{a})^2 + (\frac{y}{b})^2 = -1$, empty set
Idea of proof. Diagonalize the matrix $\svector{a & b\\b & c}$ describing the quadratic part of the above equation and then calculate translation vector $b$.
These are called conic sections, since they arise as intersections of cone of revolution (or a cylinder) with an affine plane. The cone of revolution is defined by
\[\left\{
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix} \in \R^3 | x^2 + y^2 – z^2= 0
\right\}\,.
\]
Some facts on Conic Sections
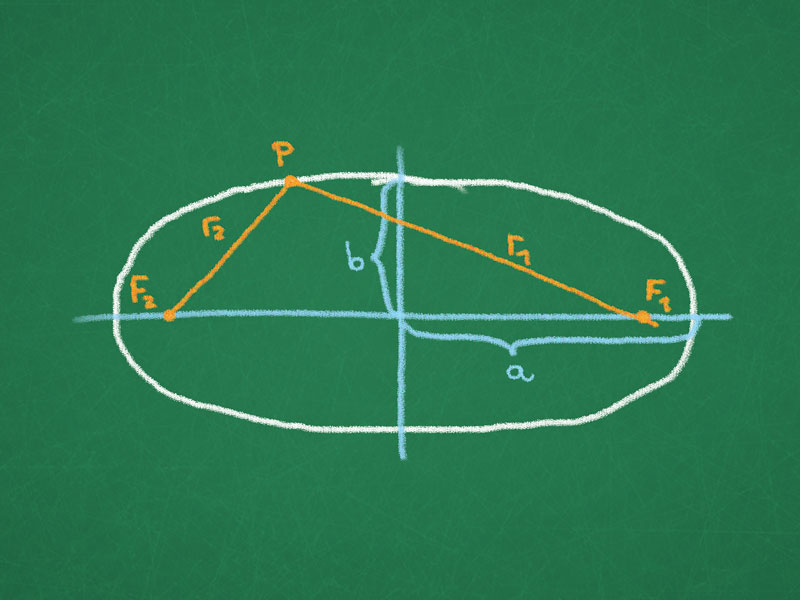
- Ellipse($a > b$),
- principle axes $a$ and $b$.
- $F_{1,2} = (\pm \sqrt{a^2 – b^2},0)$, $F_{1,2}$ are focal points.
- $r_1 + r_2 = constant$.
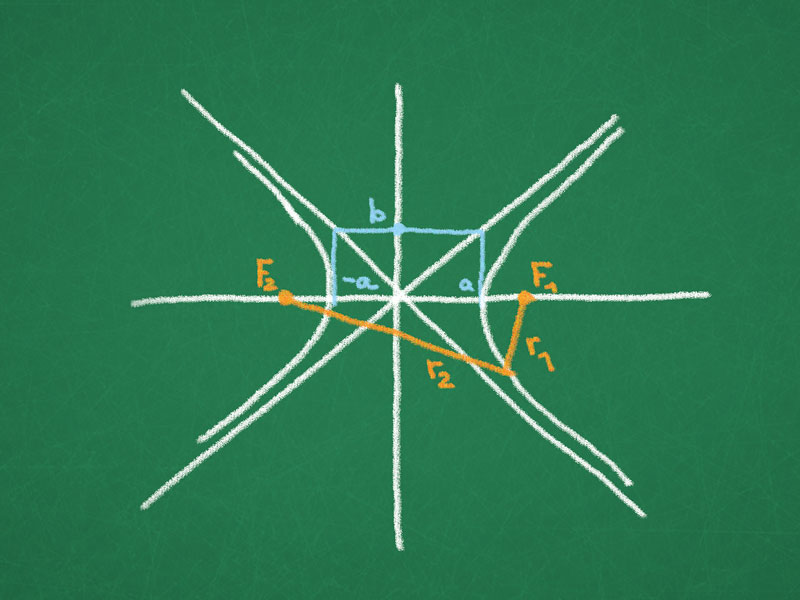
- Hyperbola
- $F_{1 2} = (\pm \sqrt{a^2 + b^2},0)$, $F_{1,2}$ are focal points.
- $\lvert r_1 – r_2 \rvert = constant$.
- Parabola
- $F = (0,\frac{1}{1+a})$, $F$ is focal point.
- $\frac{r_1}{r_2} = 1$
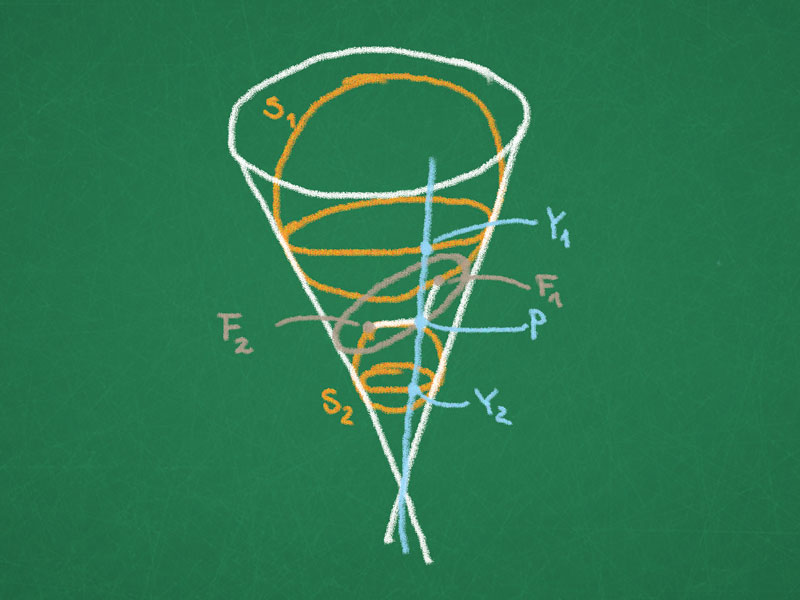
Claim. A plane cutting through the upper half of the cone of revolution and all its generating lines yields a ellipse.
Proof. Consider two spheres $S_1, S_2$ touching the cone and the plane, let $p$ be a point of intersection points of the plane and the cone. We have $\lvert F_1P\rvert = \lvert Y_1P \rvert$ and $\lvert F_2P\rvert = \lvert Y_2P \rvert$, since the tangents here have the equal length, hence, $\lvert F_1P\rvert + \lvert F_2P\rvert = \lvert Y_1P \rvert + \lvert Y_2P \rvert = \lvert Y_1Y_2\rvert = constant$.
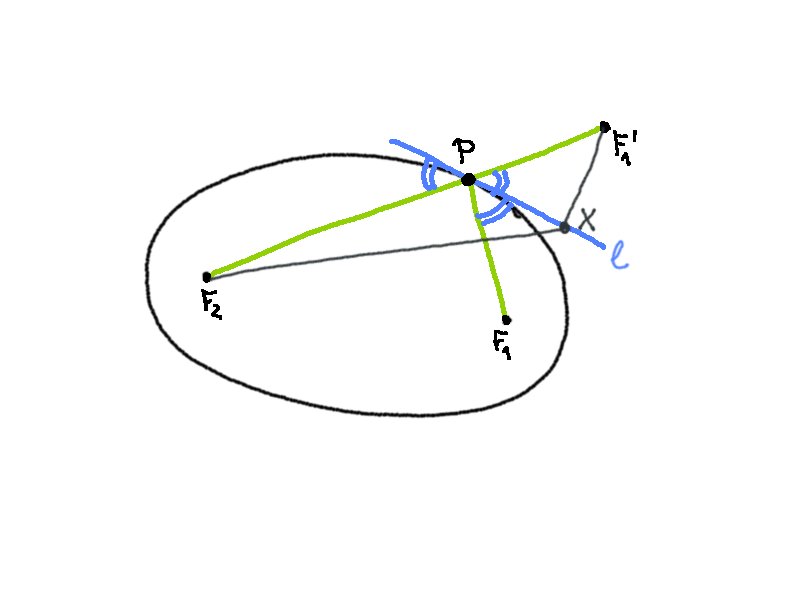
Optical properties.
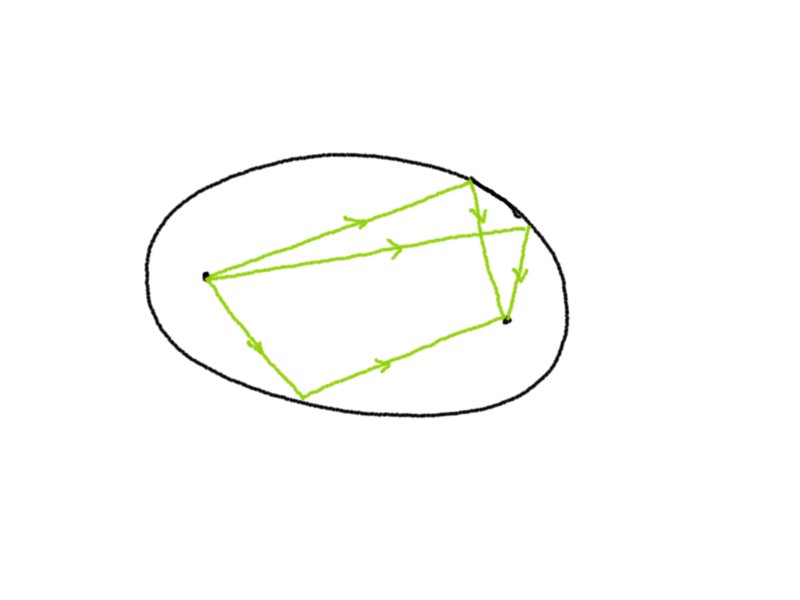
Rays emitted from one focal point of the ellipse arrive at the other focal point of the ellipse.
Proof. Consider an ellipse with foci $F_1$ and $F_2$, and a point on the ellipse $P$. Then construct the point $F_1’$ on the line $F_2P$ such that $|F_1’P| = |F_1P$. Now let $\ell$ be the angle bisector of the angle $\angle F_1PF_1’$.
We will show that $\ell$ is the tangent line. Let $X \in \ell$. Then $|F_1X| = |F_1’X|$. But by the triangle inequality we obtain
\[
|F_2X| + |F_1’X| \ge |F_2F_1’| = |F_1P| + |F_2P|
\]
with equality if and only if $X = P$. So $\ell$ is the tangent and the angles are equal.
Rays emitted from one focal point of the hyperbola are reflected such that the reflected lines go through the other focal point.
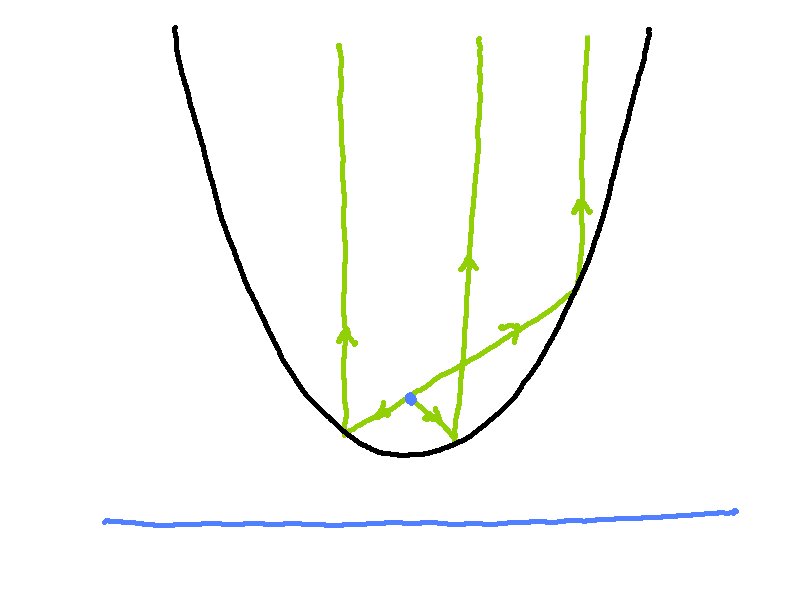
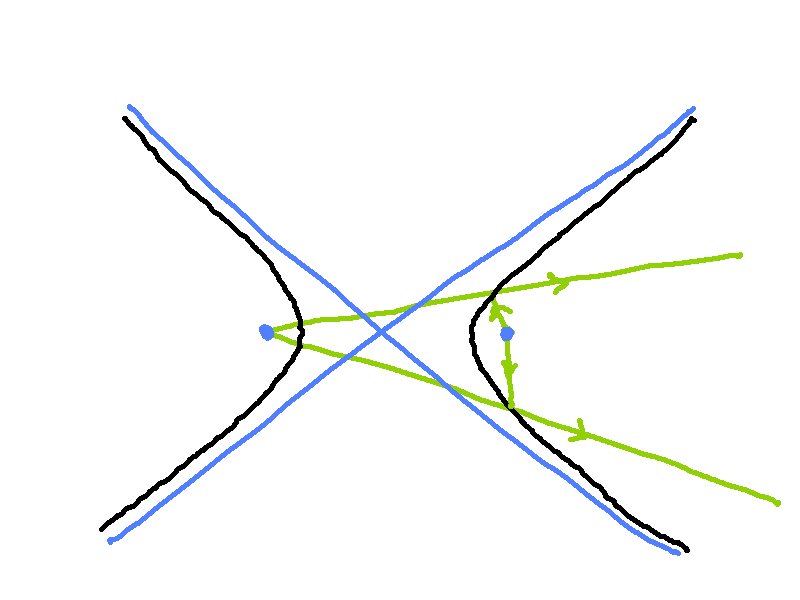 Rays emitted from the focal point of the parabola become parallel after reflection.
Rays emitted from the focal point of the parabola become parallel after reflection.