Note If a conic in $\mathbb{R}P^{2}$ contains a line, then it is degenerate.
Theorem. Through five points $P_{1},P_{2},P_{3},P_{4},P_{5} \in \mathbb{R}P^{2}$ there exists a conic in $\mathbb{R}P^{2}$.
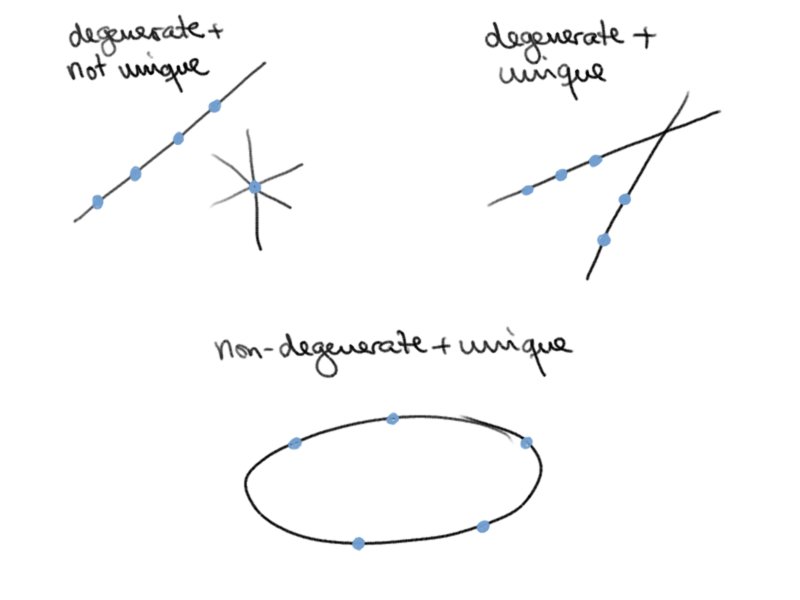
$i)$ If no four points lie on a line, then the conic is unique.
$ii)$ If no three lie on one line (five points in general position), then the conic is non-degenerate.
Lemma. If a conic contains three collinear points, then it contains the line through these points.
Proof of Theorem
Existence:
Let $P_{i}=\left[ v_{i}\right]$ with $v_{i} \in \mathbb{R}^{3} \quad \forall i=1,..,5$. Let $q: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ be a quadratic form. Then an incidence $P_{i} \in \phi = \{ \left[ x \right] \in \mathbb{R}P^{2} \left| \right. q \left( x \right) =0 \}$ yields an homogeneous equation for the corresponding matrix entries. $q \left( v_{i} \right) = 0 \Leftrightarrow v_{i}^{T} B v_{i} = 0$.
The system $q \left( v_{i} \right) = 0 \quad \forall i=1,\ldots,5$ has at least a one dimensional space of solutions. So there exists a quadratic form, such that the conic contains all $P_{i}$.
Statement $i)$:
If four of the $P_{i}$ lie on a line, then the conic contains a line and is degenerate.
In this case there exists a one parameter family of conics containing the $P_{i}$. If three points $P_{1},P_{2},P_{3}$ lie on a line $l$, but $P_{4}, P_{5} \notin l$.
Then by the Lemma $l \subset \phi$ and $\phi$ is degenerate. So the conic consists of the lines $l$ and $P_{4}P_{5}$. In particular $\phi$ is unique.
Statement $ii)$ and second part of $i)$:
Now let no three of the points be colinear and $q_{1}$ and $q_{2}$ are two quadratic forms with $q_{1}\left( v_{i} \right) = q_{2} \left(v_{2} \right) = 0$. But then the quadratic form $q=q_{1}+ \lambda q_{2}$ also satiesfies $q \left( v _{i} \right) = 0 \quad \forall i=1,…,5$. The determinant $det \left( q_{1} + \lambda q_{2} \right)$ is a polynomial in $\lambda$ of degree $3$. So it has a zero: $\exists \lambda_{0}$ such that $det\left(q_{1} + \lambda_{0} q_{2} \right) =0$ and $q_{1}+ \lambda_{0} q_{2}$ is degenerate. Thus three points must be colinear.
Widerspruch! $\Rightarrow \quad q_{1}=q_{2}$ is unique and non-degenerate. $\square$
Pencils of conics
Definition
A pencil of conics is a line in $\mathbb{R}P^{5}$, which is the space of conics in $\mathbb{R}P^{2}$. Let $\left[ q_{1} \right]$ and $\left[ q_{2} \right]$ be two conics, then the conic $\left[q\right]$ is in the pencil, if there exist homogeneous coordinates $\left(\lambda_{1} \lambda_{2}\right)$, such that $\left[q \right] = \left[ \lambda_{1} q_{1} + \lambda_{2} q_{2} \right]$.
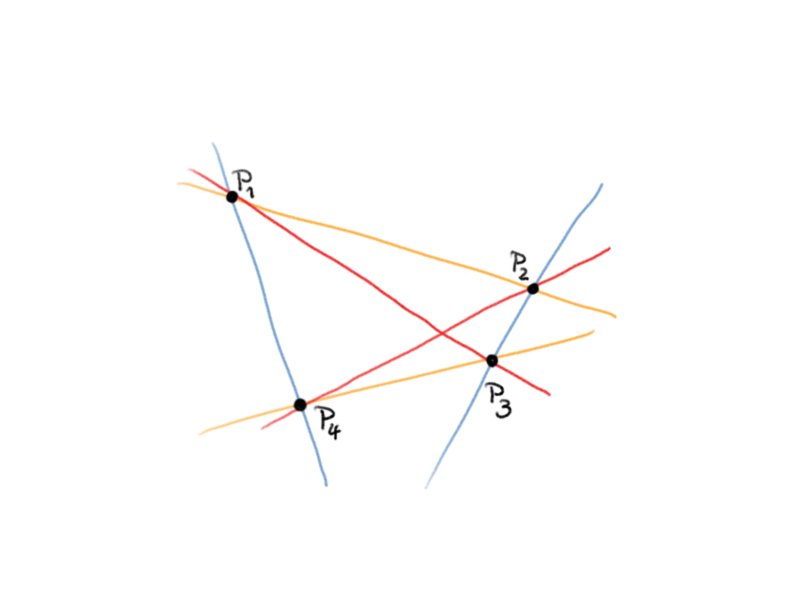
Let $P_{1},…,P_{4} \in \mathbb{R}P^{2}$ be 4 points in general position. Then the conics through these four points build a pencil.
The pencil contains three degenerate conics: $q_{1}=l_{12}l_{34},q_{2}=l_{13}l_{24}, q_{3}=l_{14}l_{23}$, where $l_{ij} : \mathbb{R}^3 \rightarrow \mathbb{R}$ is the linear function vanishing on the points $P_{i}$ and $P_{j}$. Now for an arbitrary fifth point $P_{5} \neq P_{i} \quad \forall i=1,…,4$ there exists a unique conic through $P_{1},\ldots,P_{5}$ by the last theorem.
The conics of the pencil are given by homogeneous coordinates $\left( \lambda_{1}\lambda_{2} \right)$ with $\left[q \right] = \left[ \lambda_{1} q_{1} + \lambda_{2} q_{2} \right]$. The fifth point $P_{5}=\left[v_{5}\right]$ lies on the conic if
\[ q\left(v_{5} \right) = 0 \quad \Rightarrow \quad \lambda_{1} q_{1} \left( v_{5} \right) + \lambda_{2} q_{2} \left( v_{5} \right) =0 \quad \Rightarrow \quad \lambda_{1} = q_{2} \left(v_{5} \right) \land \lambda_{2} = -q_{1} \left(v_{5} \right).\]
The conic containing $P_{5}$ in the pencil is $\left[ q \right] = \left[ q_{2} \left( v_{5} \right) q_{1} – q_{1} \left( v_{5} \right) q_{2} \right]$.
Remark of conics:
We now have found the following identifications:
quadratic form $\leftrightarrow$ symmetric bilinear forms $\leftrightarrow$ symmetric matrices $\leftrightarrow$ $\mathbb{R}^{6}$
and conis $\leftrightarrow$ quadratic forms up to skalar multiple $\leftrightarrow$ $P \left( \mathbb{R}^{6} \right) = \mathbb{R}P^{5}$
and pencils of conics $\leftrightarrow$ lines in $\mathbb{R}P^{5}$.
Pascal’s theorem
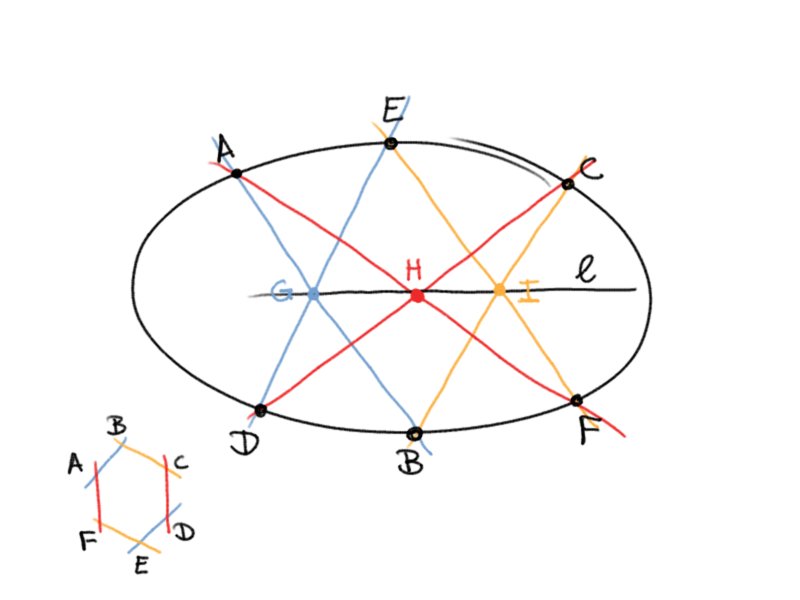
Let $A,B,C,D,E,F$ be six points on a conic. Consider the hexagon $A,B,C,D,E,F$. Then the intersection points of opposite sides are colinear. I.E. there exists a line containing $G=AB \cap DE, I=BC \cap EF, H=CD \cap AF$.
Proof:
Consider the two pencils of the conics through $A,B,C,D$ and $A,D,E,F$. Then both pencils contain the conic:
\[ q=\lambda_{1} l_{AB}l_{CD}+\lambda_{2}l_{AD}l_{BC}=\mu_{1}l_{AF}l_{DE}+\mu_{2}l_{AD}l_{EF}\]
\[\Leftrightarrow \lambda_{1} l_{AB}l_{CD} – \mu_{1}l_{AF}l_{DE}=l_{AD} \left( \mu_{2} l_{EF} – \lambda_{2} l_{BC}\right)\]
Claim:
The line containing the intersection points s given by $\mu_{2} l_{EF} – \lambda_{2} l_{BC}$.
$1.)$ $G=\left[v_{G}\right]$ is on the line, since $l_{AD}\left(v_{G}\right) \neq 0$, but $l_{AB}\left(v_{G}\right)=0$ and $l_{DE}\left(v_{G}\right)=0$.
\[\Rightarrow \left( \mu_{2} l_{EF} – \lambda_{2} l_{BC} \right) \left(v_{G} \right) =0\]
$2.)$ same with $H \quad \Rightarrow \quad H$ is on the line.
$3.)$ $I=\left[v_{i}\right]$ is on the line, since $l_{EF} \left(v_{I}\right) = 0$ and $l_{BC}\left(v_{I}\right)=0$.
$\square$
Remark. Pappus theorem corresponds to Pascal’s theorem on a degenerated conic.