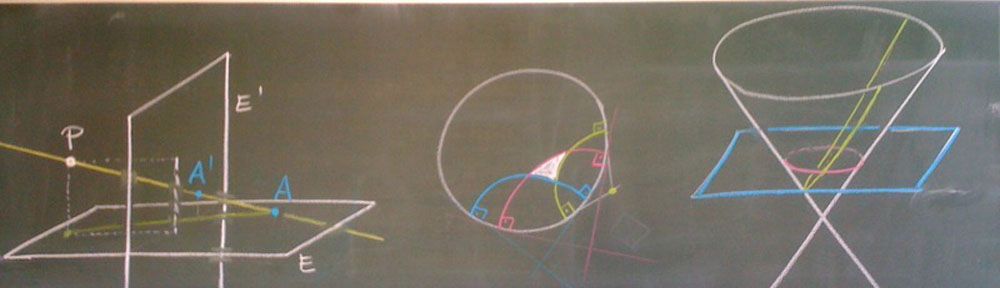Polarity: Pole – Polar Relationship
Let $b: V \times V \rightarrow \mathbb{F}$ be a symmetric non-degenerate bilinear form.
Definition. Let $U \leq V$ be a vector subspace. Then
\[
U^{\perp} = \{ v \in V \: | \: b(u,v) = 0, \: \forall u \in U \}.
\]
If $U = \{u_1,…,u_k\}$ then
\[
U^{\perp} = ( \text{span} \; U )^{\perp} = \{ v \in V \: | \: b(u_i,v) = 0, \: \forall i = 1,…,k \}.
\]
We call $U^{\perp}$ the orthogonal complement of $U$.
Remark. dim $U^{\perp} =$ dim $U^0 = n – k$, if dim $U = k$ and dim $V = n$.
Example.
- $b: \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R}$,\[
b \left( \left(
\begin{array}{c}
x_1 \\ y_1
\end{array}
\right),
\left(
\begin{array}{c}
x_2 \\ y_2
\end{array}
\right)
\right)
= x_1x_2 + y_1y_2 ,
\]with usual orthogonality and scalar product.
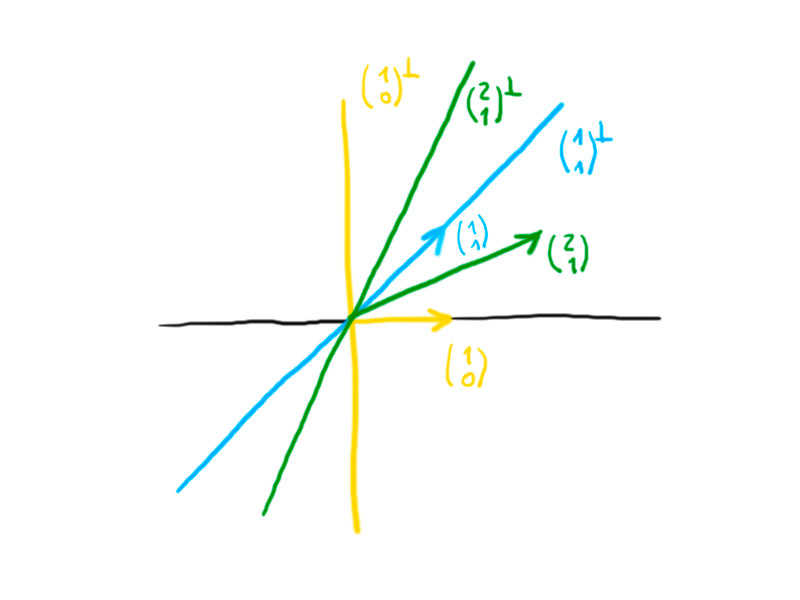
- $b: \mathbb{R}^2 \times \mathbb{R}^2 \rightarrow \mathbb{R}$,\[
b \left( \left(
\begin{array}{c}
x_1 \\ y_1
\end{array}
\right),
\left(
\begin{array}{c}
x_2 \\ y_2
\end{array}
\right)
\right)
= x_1x_2 – y_1y_2 ,
\]\[
\left(
\begin{array}{c}
1\\0
\end{array}
\right)^{\perp} =
\left\{ \left. \left(
\begin{array}{c}
x\\y
\end{array}
\right) \: \right| \:
0 = b
\left( \left(
\begin{array}{c}
1\\0
\end{array}
\right),
\left(
\begin{array}{c}
x\\y
\end{array}
\right) \right)
= x \right\},
\]\[
\left(
\begin{array}{c}
1 \\ 1
\end{array}
\right)^{\perp} =
\left\{ \left. \left(
\begin{array}{c}
x \\ y
\end{array}
\right) \: \right| \:
x – y = 0
\Leftrightarrow
x = y
\right\},
\]\[
\left(
\begin{array}{c}
1 \\ 2
\end{array}
\right)^{\perp} =
\left\{ \left. \left(
\begin{array}{c}
x \\ y
\end{array}
\right) \: \right| \:
x – 2y = 0
\right\},
\]
for example, take $x = 2, y = 1$.
- If $b$ is indefinite, (i.e. signature contains $+$’s and $-$’s), then there exist vectors $v$ with $b(v,v) = 0$. These are called isotropic vectors.
- In example 2, if we restrict to the subspace $\left\{ \lambda \left(\begin{array}{c} 1 \\ 1 \end{array} \right) \: \left| \: \lambda \in \mathbb{R} \right. \right\}$, the non-degenerate bilinear form restricted to this subspace is degenerate!
\[
\left\{ \left( \begin{array}{c} -1 \\ 1 \end{array} \right), \left( \begin{array}{c} 1 \\ 1 \end{array} \right) \right\} \Rightarrow \left( \begin{array}{cc} 0 & -1 \\ -1 & 0 \end{array} \right).
\]
Polarity in $\mathbb{R}P^2$.
Using the orthogonal complement, we define a map:
\[
[p] \mapsto \text{line,} \: \text{namely}: \: P(\{\lambda p\} ) \mapsto P(\{p\}^{\perp}).
\]
\[
\ell \mapsto \text{point,} \: \text{namely}: \: P(U) \mapsto P(U^{\perp}).
\]
Definition. The line corresponding to a point is the polar (or polar line) of $[p]$ and $[p]$ is the pole.
Geometry of pole-polar relationship
Up to projective transformations, there is only one non-degenerate, non-empty conic in $\mathbb{R}P^2$.
It corresponds to a non-degenerate symmetric indefinite bilinear form with signature (+ + -), (- – +).
Definition. A line in $\mathbb{R}P^2$ is a tangent to a conic if it has one point in common with the conic or lies entirely in the conic.
Proposition. The polar line of a point $[p]$ on a conic is a tangent at this point.
Proof. Let $\mathscr{C} = \{[x] \in \mathbb{R}P^2 \: | \: b(x,x) = 0\}$. The polar line to $[p]$ is
\[
P(\{p\}^{\perp}) = \{[x] \in \mathbb{R}P^2 \: | \: b(p,x) = 0 \}.
\]
- $p$ lies on the polar, since $b(p,p) = 0 \Leftarrow [p] \in \mathscr{C}$.
- now let $[q] \in \mathbb{R}P^2$ with $b(p,q) = 0$.
The polar line is given by: $[\lambda p + q]$ (except $[p]$).
\[ \begin{array}{ccccccc}
\Rightarrow b(\lambda p + q, \lambda p + q) & = & \lambda^2 b(p,p) & + & 2\lambda b(p,q) & + & b(q,q) \\
& = & 0 & + & 0 & + & b(q,q).
\end{array}
\]
\[ \begin{array}{ccl}
\text{If} \: b(q,q) = 0, & \Rightarrow & b(\lambda p + q, \lambda p + q) = 0 \qquad \forall \lambda \in {\bf R}, \\
& \Rightarrow & \text{The polar is contained in } \mathscr{C}.
\end{array}
\]
\[ \begin{array}{ccl}
\text{If} \: b(q,q) \neq 0, & \Rightarrow & b(\lambda p + q, \lambda p + q) \neq 0 \\
& \Rightarrow & \text{The polar is tangent at } [p].
\end{array}
\]
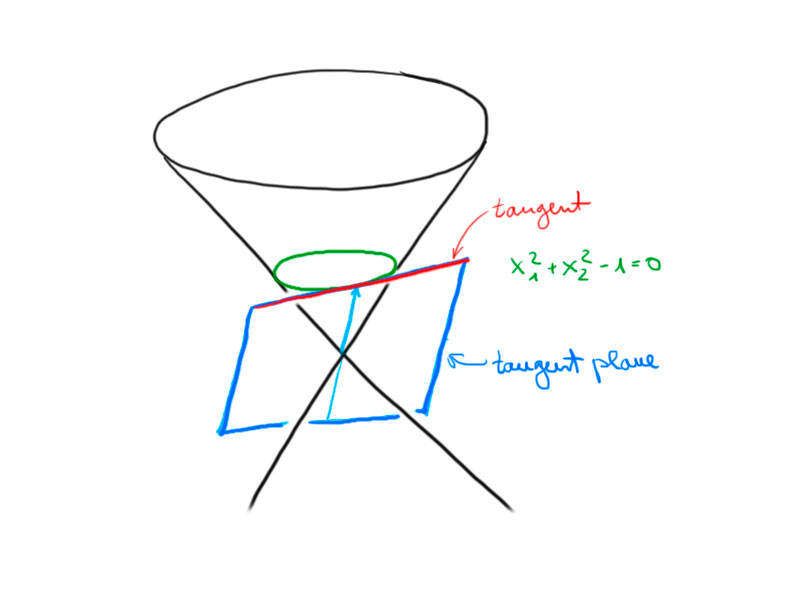
Example.
\[
b \left( \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right), \left( \begin{array}{c} y_1 \\ y_2 \\ y_3 \end{array} \right) \right) = x_1y_1 + x_2y_2 – x_3y_3.
\]
in affine coordinates:
\[
u_1 = \frac{x_1}{x_3}, \quad u_2 = \frac{x_2}{x_3},
\]
we get the conic,
\[
\mathscr{C} = \left\{ \begin{array}{c} u_1 \\ u_2 \end{array} \: \left| \: u_1^2 + u_2^2 = 1 \right. \right\}.
\]
Parametrisation:
\[
\gamma (\alpha) = \left( \begin{array}{c} u_1 \\ u_2 \end{array} \right) = \left( \begin{array}{c} \text{cos}\alpha \\ \text{sin}\alpha \end{array} \right).
\]
Tangent at $\gamma(\alpha_0)$ is:
\[
\gamma(\alpha_0) + t \gamma ‘ (\alpha_0) = \gamma(\alpha_0) + t \left( \begin{array}{c} -\text{sin} \alpha_0 \\ \text{cos}\alpha_0 \end{array} \right)
\]
\[
\lambda = \left( \begin{array}{c} \text{cos}\alpha \\ \text{sin}\alpha \\ 1 \end{array} \right).
\]
\[
U^{\perp} = \left\{ \left( \begin{array}{c} x \\ y \\ z \end{array} \right) \: \left| \: b\left( \left( \begin{array}{c} \text{cos}\alpha \\ \text{sin}\alpha \\ 1 \end{array} \right), \left( \begin{array}{c} x \\ y \\ z \end{array} \right) \right) = 0 \right. \right\}.
\]
\[
(\Leftrightarrow x \text{ cos}\alpha + y\text{ sin}\alpha – z = 0)
\]
\[
= \left\{ \lambda \left( \left. \begin{array}{c} \text{cos}\alpha \\ \text{sin}\alpha \\ 1 \end{array} \right) + \mu \left( \begin{array}{c} -\text{sin}\alpha \\ \text{cos}\alpha \\ 0 \end{array} \right) \: \right| \lambda, \mu \in {\bf R} \right\}.
\]