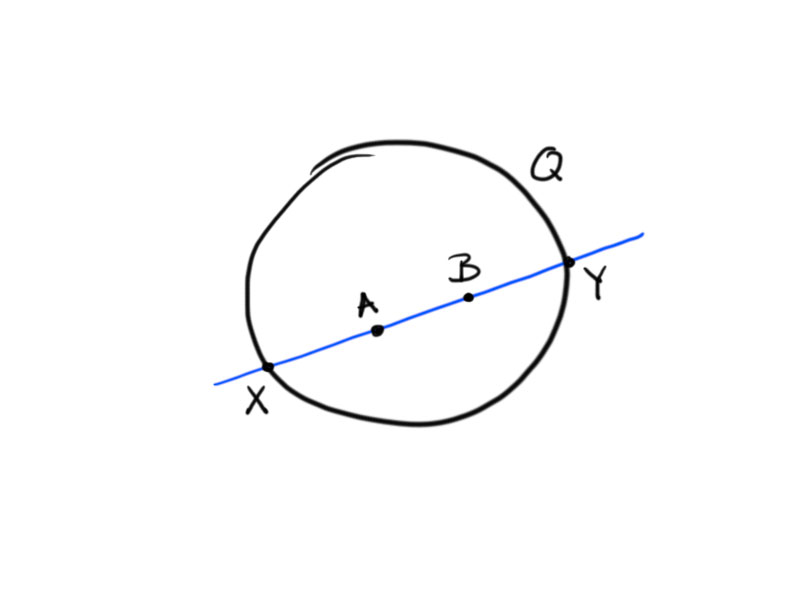
Theorem. For two points $A,B\in H_{\mathrm{pr}}^n$ let $X$, $Y$ be the points of intersection of the line $AB$ with the quadric $Q=\{[x]:\langle x,x\rangle_{n,1}=0\}$, such that $\{A,Y\}$ and $\{B,X\}$ separate each other.
Then
\[d_{\mathrm{pr}}(A,B)=\frac12\log\cr(B,X,A,Y)\,.\]

Proof.
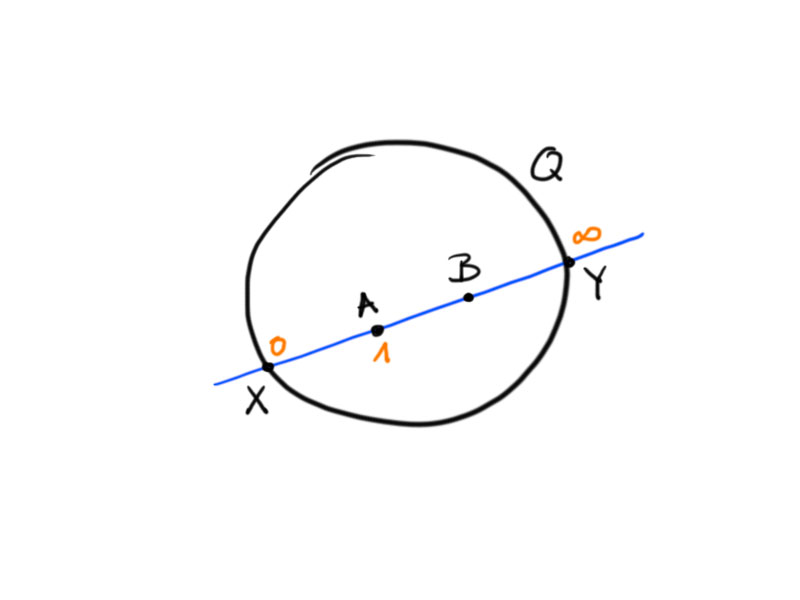
Remember that $\cr(q,1,0,\infty)=q$.
If we choose an affine coordinate such that $X=0$, $A=1$ and $Y=\infty$, then we see that $\cr(B,X,A,Y)>1$, i.e. $\log\cr(B,X,A,Y)>0$.

Parametrize $AB$ by $[a+tb]$ where $A=[a]$ and $B=[b]$.
Solving
\begin{equation}\langle a+tb,a+tb\rangle_{n,1}=0\label{ZeroesForXY}\end{equation}
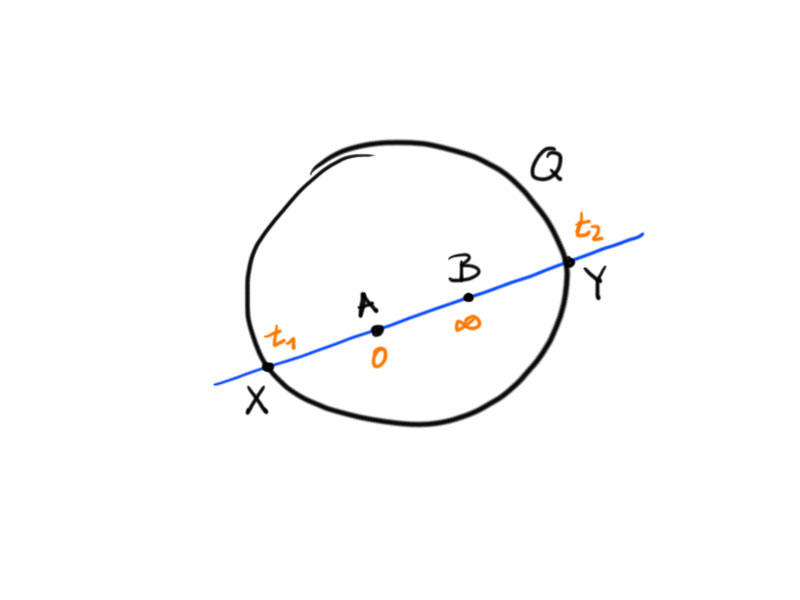
yields the two solutions $t_1$, $t_2$ such that $X=[a+t_1b]$ and $Y=[a+t_2b]$.

We have $t_1t_2>0$ and: If $t_1,t_2>0$ then $t_2>t_1$, i.e. $\frac{t_2}{t_1}>1$ — if $t_1,t_2<0$ then $t_1>t_2$ and thus again $\frac{t_2}{t_1}>1$.
Looking back at the equation above gives us
\[0=\langle a+tb,a+tb\rangle=\langle b,b\rangle t^2+2t\langle a,b\rangle+\langle a,a\rangle=\langle b,b\rangle(t-t_1)(t-t_2)\,.\]
Comparing the coefficients yields
\begin{align*}
2\langle a,b\rangle&=-\langle b,b\rangle(t_1+t_2)&
\langle a,a\rangle&=\langle b,b\rangle t_1t_2\,,\quad
\text{i.e}\\
t_1+t_2&=-2\frac{\langle a,b\rangle}{\langle b,b\rangle}&
t_1t_2&=\frac{\langle a,a\rangle}{\langle b,b\rangle}\,.
\end{align*}
Thus
\[\cosh d_{\mathrm{pr}}(A,B)=\frac{\lvert\langle a,b\rangle\rvert}{\sqrt{\langle a,a\rangle\langle b,b\rangle}}=\frac{\lvert t_1+t_2\rvert}{2\sqrt{t_1+t_2}}\,.\]
The cross ratio is
\[\cr(B,X,A,Y)=\cr(\infty,t_1,0,t_2)=\frac{\infty-t_1}{t_1-0}\frac{0-t_2}{t_2-\infty}=\frac{t_2}{t_1}\,.\]
This implies
\begin{align*}\cosh\frac12\log\cr(B,X,A,Y)
&=\frac12\left(\mathrm e^{\frac12\log\frac{t_2}{t_1}}+\mathrm e^{-\frac12\log\frac{t_2}{t_1}}\right)=\frac12\left(\sqrt{\frac{t_2}{t_1}}+\sqrt{\frac{t_1}{t_2}}\right)\\
&=\frac12\frac{\lvert t_2\rvert+\lvert t_1\rvert}{\sqrt{t_1t_2}}=\frac12\frac{\lvert t_1+t_2\rvert}{\sqrt{t_1t_2}}\,,
\end{align*}
since $t_1t_2>0$.

Lines in the hyperbolic plane

Hyperbolic lines are secants of the unit ball

Obviously, to a line and a point in $H^2$ there exist many lines through the point that do not intersect the line:

This contradicts the Parallel Axiom.

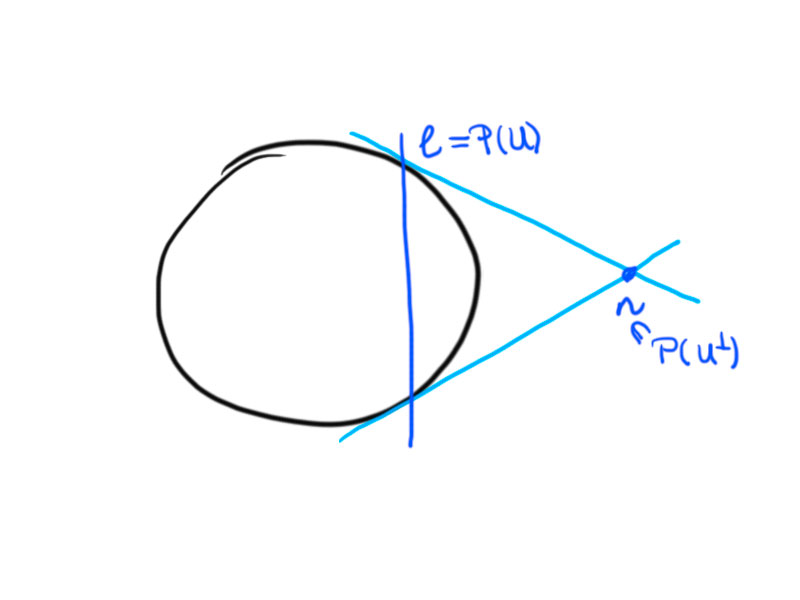
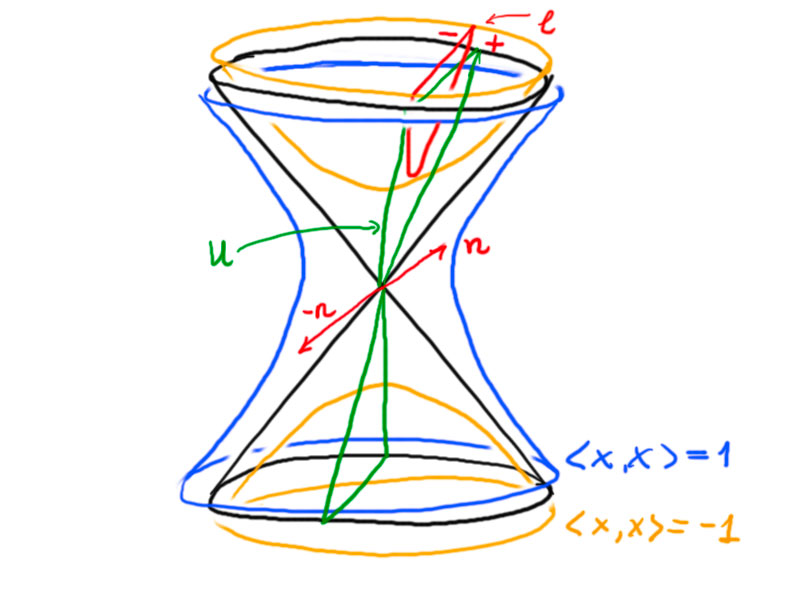
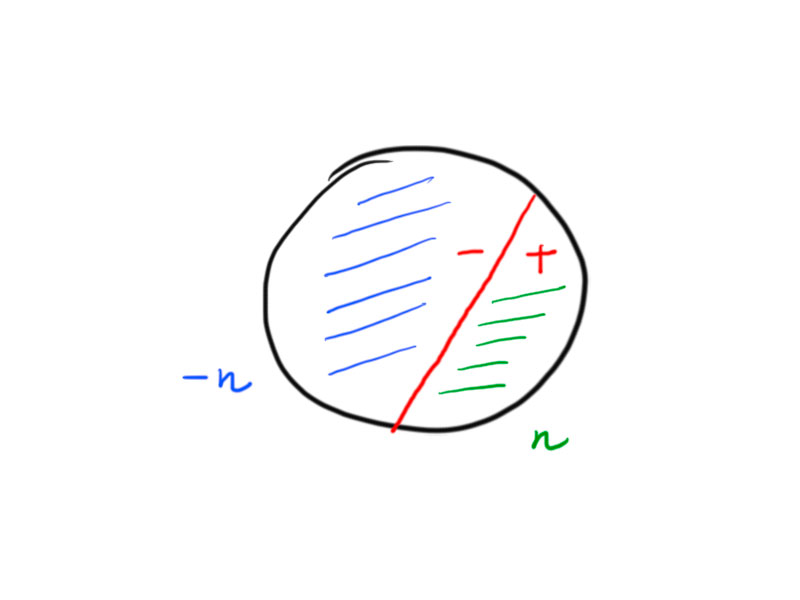
Using polarity, we can assign unit normal vectors to hyperbolic lines in $H^2$.

With $\ell=P(U)$, where $U$ is a two-dimensional subspace with signature $(+-)$ (where by the signature of a subspace $V$ we denote the signature of $\langle\cdot\,,\cdot\rangle$ restricted to $V$) we have $n\in P(U^\perp)$, where $U^\perp$ has signature $(+)$ – so we can choose $n$ with $\langle n,n\rangle=1$.
For every line there exist two unit normal vectors defined via polarity with respect to $\langle\cdot\,,\cdot\rangle_{n,1}$.
There is a bijection between half planes and vectors $n\in\R^{2,1}$ with $\langle n,n\rangle=1$.

Proposition
Let $\ell_1,\ell_2\in H^2$ be two distinct lines in the hyperbolic plane with unit normals $n_1$, $n_2$ (i.e. $\langle n_1,n_1\rangle=1$ and $\langle n_1,p\rangle=0$ for all $p\in\ell_1$).
Then the following are equivalent:

1. The two lines intersect.
2. $\operatorname{span}(n_1,n_2)$ has signature $(++)$.
3. $\lvert\langle n_1,n_2\rangle_{2,1}\rvert<1$.

Proof
(i)$\Rightarrow$(ii): Let $\ell_1\cap\ell_2=:x$.
Then $\operatorname{span}\{x\}$ has signature $(-)$, since $\langle x,x\rangle=-1$.
Thus $\operatorname{span}\{x\}^\perp$ has signature $(++)$ and $n_1,n_2\in\operatorname{span}\{x\}^\perp$.
This implies $\operatorname{span}\{n_1,n_2\}=\operatorname{span}\{x\}^\perp$ has signature $(++)$.

(ii)$\Rightarrow$(i) can be shown similarly.

(ii)$\Leftrightarrow$(iii):
The matrix for $\langle\cdot\,,\cdot\rangle\big\vert_{\operatorname{span}\{n_1,n_2\}}$ is given by
\[A=\begin{pmatrix}\langle n_1,n_1\rangle&\langle n_1,n_2\rangle\\\langle n_1,n_2\rangle&\langle n_2,n_2\rangle\end{pmatrix}=\begin{pmatrix}1&\langle n_1,n_2\rangle\\\&1\end{pmatrix}\,.\]
$A$ is positive definite if and only if $\operatorname{span}\{n_1,n_2\}$ is $(++)$, which is (ii).
But also, positive definiteness if equivalent to $1>0$ and $1-\langle n_1,n_2\rangle^2>0$, which is (iii).