Stereographic projection
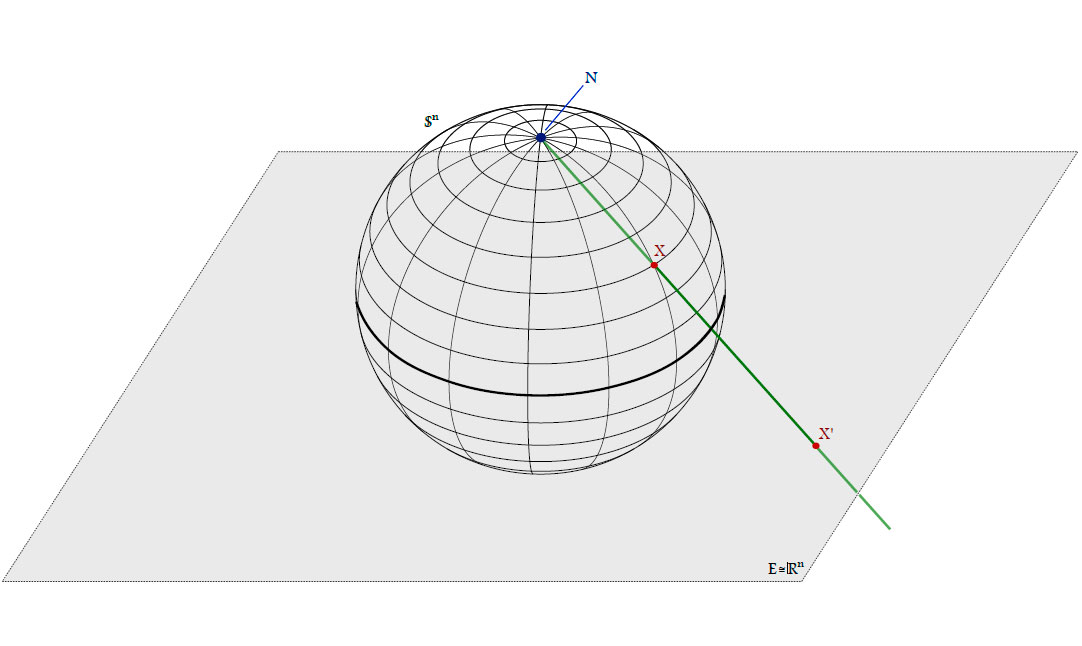
Definition. Denote the unit sphere in $\mathbb{R}^{n+1}$ by $\mathbb{S}^{n}=\left\{{x \in \mathbb{R}^{n+1}|(x,x)=1}\right\}$ and its north pole by $\mathbf{N}=e_{n+1}$.
The stereographic projection is a map $\sigma\colon \mathbb{S}^{n}\to\mathbb{R}^{n} \cup \left\{{\infty}\right\}$ from $\mathbf{N}$ to the plane
$E=\left\{{x \in \mathbb{R}^{n+1}|x_{n+1}=0}\right\} \cong \mathbb{R}^{n}$ through the equator:
\[
\sigma(X)=
\left\{
\begin{array}{ll}
\infty & \textrm{, } X = \mathbf{N}\\
l_{NX}\cap E & \textrm{, } X \neq \mathbf{N}\\
\end{array}
\right.
\]
Analytically $\sigma$ is given by
\[
\sigma(X)= \sigma\ \left(\begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix} \right)
= \frac{1}{1-x_{n+1}}\begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix}
\]
since
\[N+\lambda(X-N)=e_{n+1}+\lambda \begin{pmatrix}
x_1\\\vdots\\x_{n+1}
\end{pmatrix}
= \begin{pmatrix}
y_1\\\vdots\\y_{n}\\0
\end{pmatrix}
\Rightarrow \lambda=-\frac{1}{x_{n+1}-1}=\frac{1}{1-x_{n+1}}, X\neq N.
\]
Sphere inversion
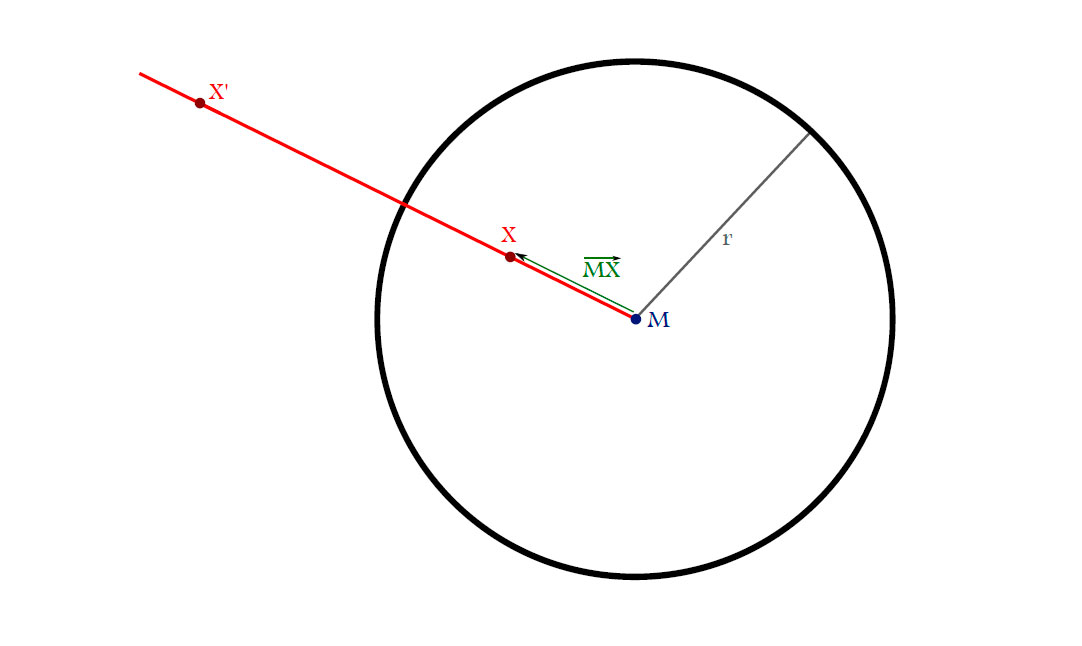
Definition. The sphere inversion $i_{M,r}\colon \mathbb{R}^{n} \cup \left\{{\infty}\right\} \to \mathbb{R}^{n} \cup \left\{{\infty}\right\}$ in the sphere
$\mathbf{S}_{M,r}=\left\{{x \in \mathbb{R}^{n}|\left\|x-M\right\|=r}\right\}$ is given by the following conditions:
- $X’$ lies on the ray $\overrightarrow{MX}$,
- $\left\|M-X\right\|\left\|M-X’\right\|=r^2$,
- $M\longleftrightarrow\infty$.
Properties of sphere inversions
- $i_{M,r}$ is an involution,
- $\mathbf{S}_{M,r}$ is fixed,
- affine subspaces containing M are mapped onto themselves.
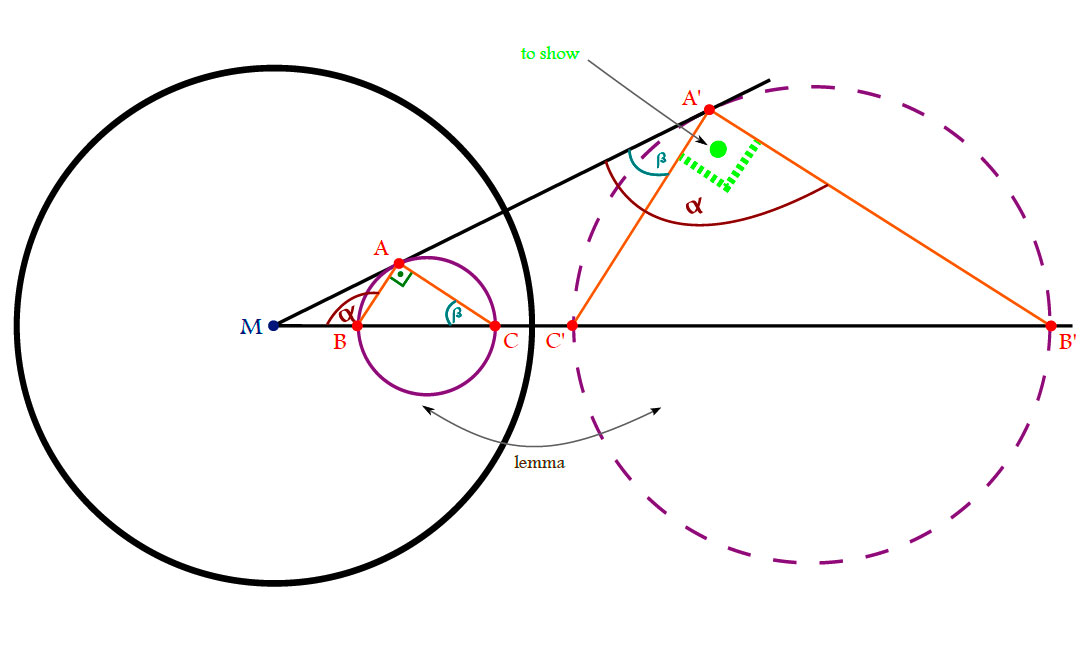
Lemma.
Proof.
Since
\[
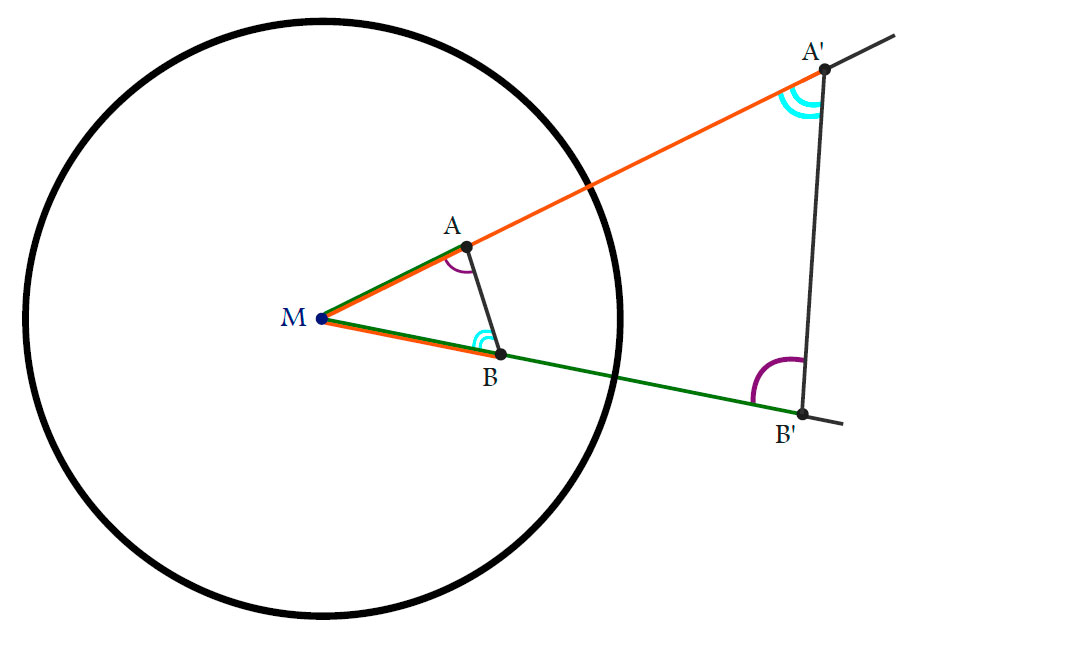
\left\|M-A\right\|\left\|M-A’\right\|=r^2 = \left\|M-B\right\|\left\|M-B’\right\| \iff
\frac{\left\|M-A\right\|}{\left\|M-B\right\|}=\frac{\left\|M-B’\right\|}{\left\|M-A’\right\|}
\]
we get that $\Delta AMB$ and $\Delta B’MA’$ are similar. In particular:
\[
\measuredangle MA’B’=\measuredangle ABM.
\measuredangle MAB=\measuredangle A’B’M.
\]
$\Box$
Corollary. Circles through M are mapped to lines. In particular, the line is parallel to the tangent to the circle at M.
Remark. All lines are thought to contain the point $\infty$ and are considered as circles of infinte radius.
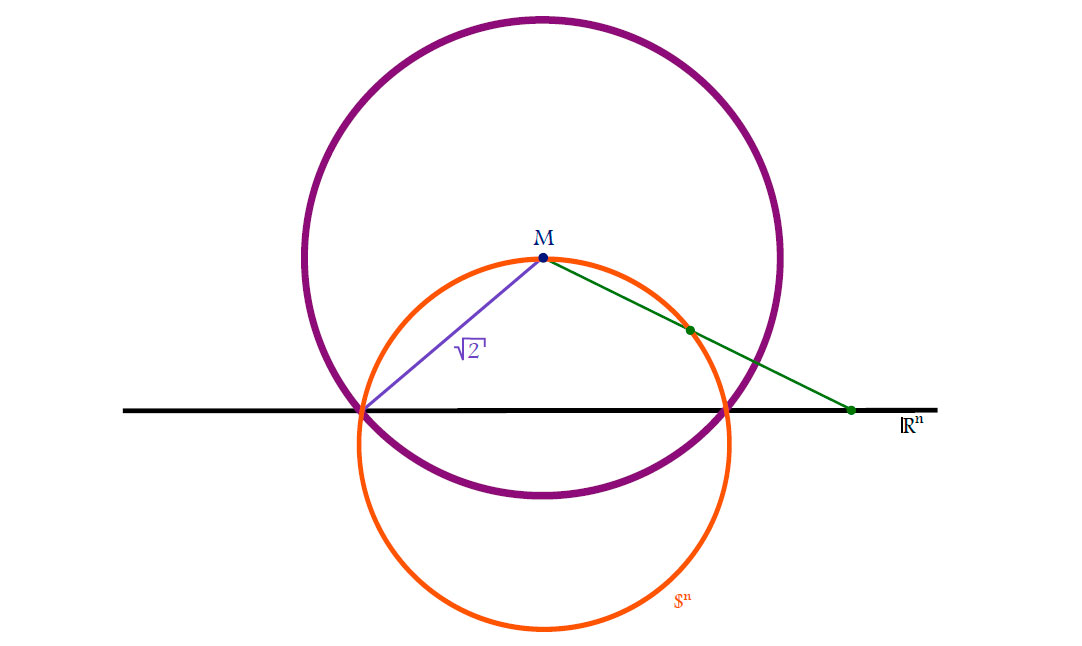
Corollary. The stereographic projection is the restriction of the sphere inversion $i_{M,r}$ with $M=e_{n+1}$ and $r=\sqrt{2}$.
Proof.
- The equator of $\mathbb{S}^{n}$ is fixed.
- $\mathbb{S}^{n}$ is mapped to a plane (Corollary) through the equator (1).
- Both inversion and stereographic projection preserve the rays.
- The intersection points of a ray with $\mathbb{S}^{n}$ and $\mathbb{R}^{n}$ are unique, hence $i_{M,r}\Big|_{\mathbb{S}^{n}}=\sigma$.
- $N=M\longrightarrow\infty$ by $i_{M,r}$.
$\Box$
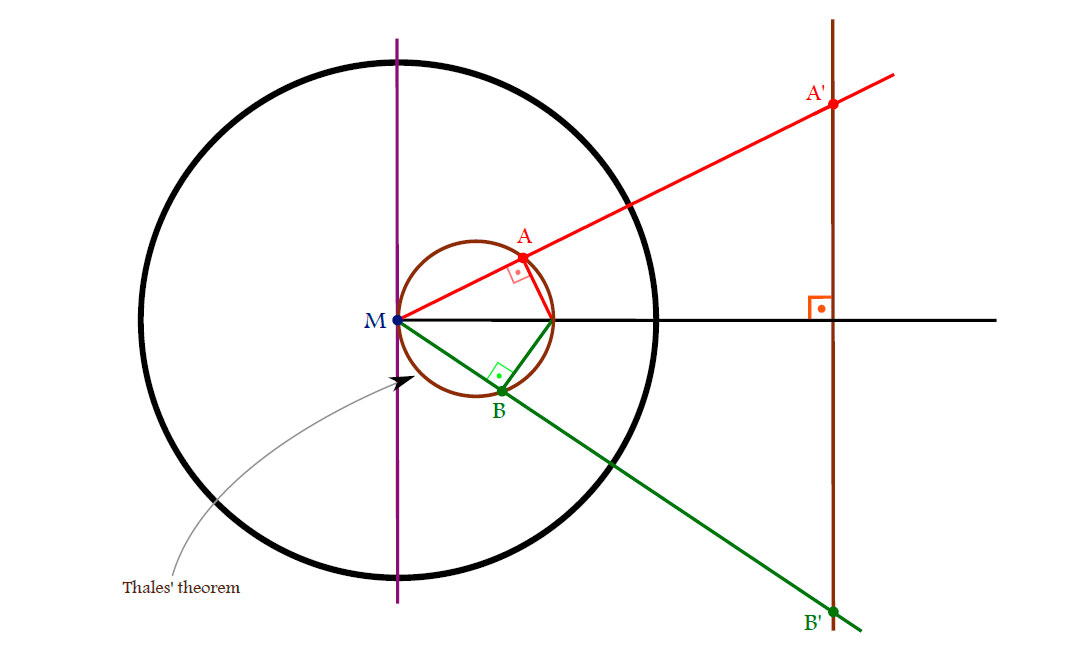
Theorem. An inversion in a sphere:
- maps spheres/hyperplanes to spheres/hyperplanes,
- is a conformal map, i.e. it preserves angles.
Proof.
(i) Consider the following sketch:
Hence the angles $\alpha$ and $\beta$ satisfy
\[
(\pi-\alpha)+\beta+\frac{\pi}{2}=\pi \Rightarrow \alpha-\beta=\frac{\pi}{2}.
\]
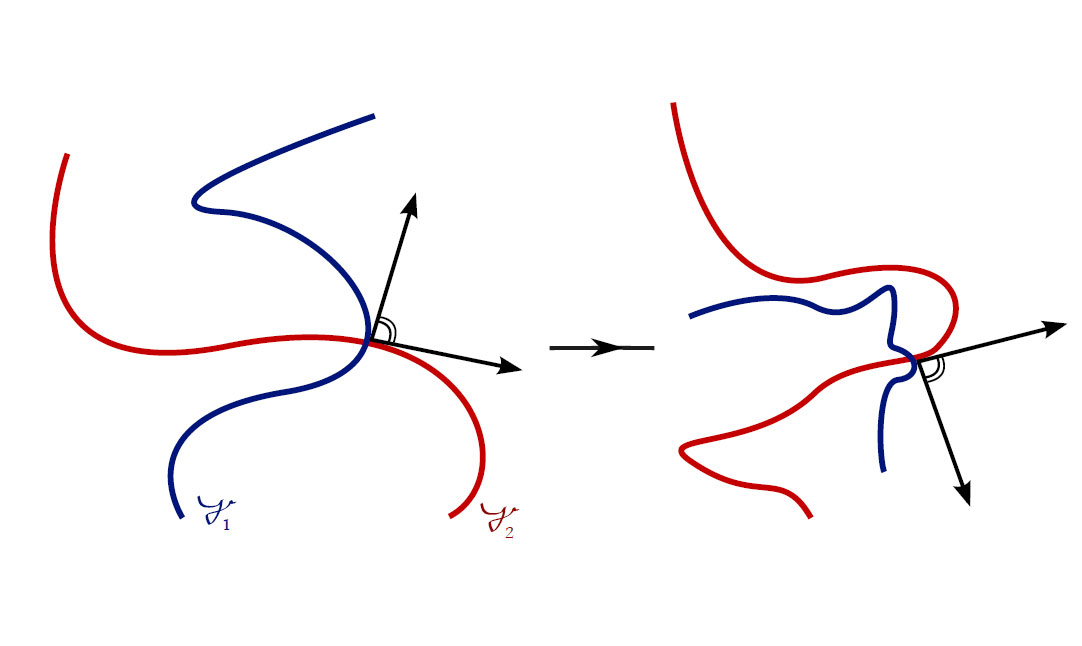
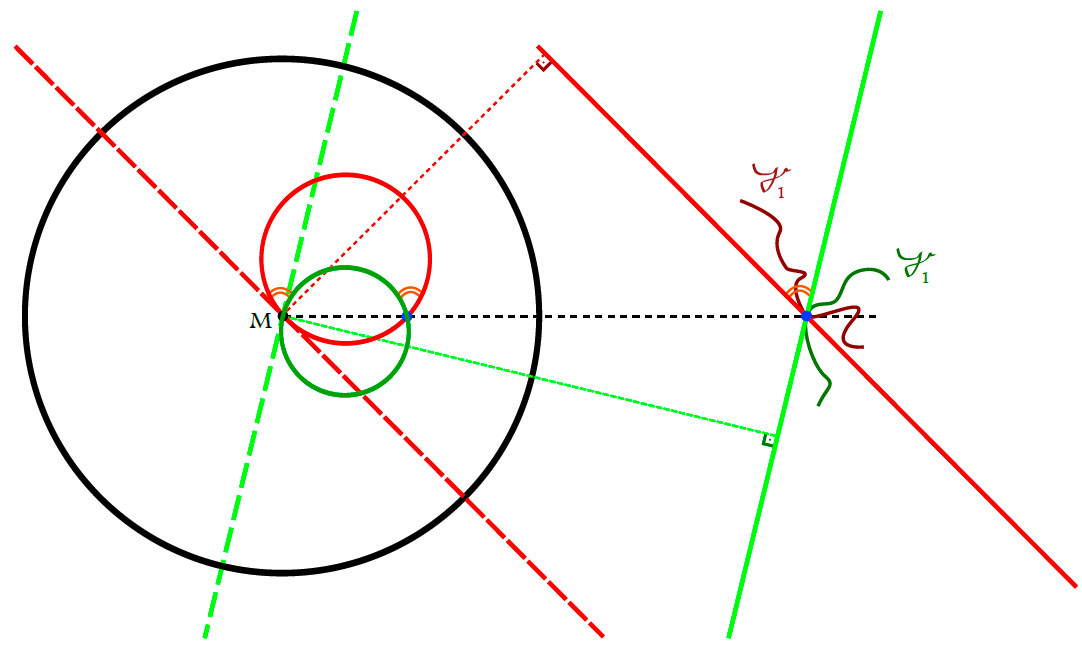
(ii) Conformality follows from the following picture
$\Box$
Remark. In general, the center of a sphere is not mapped to the center of its image by an inversion.
Corollary.
- The stereographic projection maps spheres through the north pole to hyperplanes and spheres not through the north pole to spheres.
- All spheres/hyperplanes are images of spheres on $\mathbb{S}^{n}$ under $\sigma$ (because $i_{0,1}$ is an involution).
- $\sigma$ is conformal.
Formula for the sphere inversion.
Consider the second figure showing the general idea of a sphere inversion. Since $X’$ lies on the ray $XM$ we have $X’=M+\lambda(X-M), \lambda > 0$ and from the second requirement for the sphere inversion we obtain
\begin{align*}
&&\underbrace{\left\|X’-M\right\|}_{X’-M=\lambda(X-M)} \left\|X-M\right\|&=r^2\\
\Rightarrow&& \lambda \left\|X-M\right\| \left\|X-M\right\|&=r^2\\
\Rightarrow&& \lambda = \frac{r^2}{\left\|X-M\right\|^2}.
\end{align*}
Hence the sphere inversion is given by
\[
i_{M,r}=M+\frac{r^2}{\left\|X-M\right\|^2}(X-M).
\]