Monthly Archives: April 2013

Tractrices and Darboux Transforms

Leave a reply

Let us investigate the tracks traced out by the wheels of a moving bicycle during some time interval $[a,b]$. We denote the path of the (center of the) rear wheel  by $\tau$ and the path of the front wheel by $\gamma$. If $\ell$ is the distance between the rear and the front wheel then at each time $t$ the direction of the bicycle is given by a unit vector $T(t)$ such that

\[\gamma=\tau+\ell\, T.\]

In the picture below the front wheel $\gamma$ moves on a straight line. The resulting path of the rear wheel is called the tractrix curve and has been investigated already in 1676 by Isaac Newton and in 1692 by Christian Huygens.

bicycle

 

Assuming that the rear wheel rolls without sliding it must move in the direction of $T$: There is a function $\rho: [a,b] \to \mathbb{R}$ such that

\[\tau’=\rho T.\]

Suppose the bicycle is prolonged in the rear direction by a rod. We assume that the tip of the rod has distance $\ell$ to the center of the rear wheel (only projections to the horizontal plane are considered here). Then the position $\eta(t)$ of the tip of the rod is given as

\[\eta=\tau-\ell T.\]

The rotation speed $\omega(t)$ of the bicycle is defined via

\[T’=\omega JT.\]

From

\begin{align*}\gamma’ &= \rho’ T+\ell \omega JT \\\\ \eta’ &= \rho’ T-\ell \omega JT \end{align*}

it is easy to see that the velocity vector $\eta’$ of the back end is equal in magnitude to the speed $\gamma’$ of the front wheel:

\[|\eta’|^2=\rho’^2+\omega^2=|\gamma’|^2.\]

Moreover, if we were to install another wheel at the rear end that also rolls without sliding it would have to make the same angle (though opposite in direction) with the bicycle as the front wheel. Such a bicycle (omitting the middle wheel) has in fact been built, even though I have to admit that the video does not look convincing.

On the other hand, cars with four-wheel steering are manufactured in some variety. The motion of cars with four wheels is more difficult to analyze, but to some approximation we might assume also here that the center $\tau$ of the rear axis moves towards the center $\gamma$ of the front axis. The right picture below shows a DAF MC-139 prototype from 1940 (yes, it has two driver seats). The model in the left picture even has the middle wheels (showing the tractrix) and a video can be found here.

vehicles

Let us condense all this into a mathematical

Definition: Let $\tau: [a,b]\to \mathbb{R}^n$ be a path and suppose there are $T:[a,b] \to\mathbb{R}^n$ of unit length $|T|=1$ and $\rho: [a,b] \to \mathbb{R}$ such that $\tau’=\rho T$. Then for every $\ell\in \mathbb{R}$ the path $\tau$ is called a tractrix of the path $\gamma:=\tau+\ell\,T$. Furthermore $\eta:=\tau-\ell\,T$ is called a Darboux transform of $\gamma$.

It is easy to see that in the above situation $\tau$ is a tractrix also of $\eta$ and $\gamma$ also is a Darboux transform of $\eta$. The paths $\gamma$ and $\eta$ always have the same length. Note that if $\gamma$ is regular then so is $\eta$ and if $\gamma$ is parametrized by arclength then the same holds for $\eta$.

We can apply similar definitions in the case of closed curves by assuming that $\tau$, $T$ and $\rho$ are periodic functions.

Theorem: Suppose $\eta$ is a Darboux transform of a periodic path $\gamma$ in $\mathbb{R}^n$ that is parametrized by arc length. Then $\gamma$ and $\eta$ have the same length and the same total squared curvature

\[\oint |\gamma”|^2=\oint |\eta”|^2.\]

If $n=3$ then $\gamma$ and $\eta$ have the same area vector

\[\frac{1}{2}\oint \gamma \times \gamma’ = \frac{1}{2}\oint \eta \times \eta’.\]

Proof: We have

\[\gamma’=\rho T + \ell T’\]

and we may assume that $\gamma$ and $\eta$ are parametrized by arc length, i.e.

\[\rho^2+\ell^2|T’|^2=1.\]

Then

\[\gamma”=\rho’T+\rho T’+\ell T”\]

and

\[\oint \langle \gamma”,\gamma”\rangle =\oint \rho’^2 + 2\ell \langle \rho’ T +\rho T’,T”\rangle +\ell^2 |T”|^2.\]

We want to show that this expression is unchanged if we replace $\ell$ by $-\ell$, i.e.

\[\oint  \langle \rho’ T +\rho T’,T”\rangle = \oint -\rho’ \langle T’,T’ \rangle – \frac{\rho}{2}\langle T’,T’\rangle’ =\oint  \rho'(\rho^2-1)+\rho^2\rho’=0.\]

Here we have used $0=\langle T,T’\rangle’=\langle T’,T’\rangle+\langle T,T”\rangle$, the equation $\rho^2+\langle T’,T’\rangle =1$ and its derivative $2\rho \rho’+\langle T’,T’\rangle’=0$.

Next we look at the area vector

\[\oint \gamma \times \gamma’ = \oint (\tau+\ell T)\times (\rho T+\ell T’).\]

Again we only have to show that the coefficient of $\ell$ vanishes, i.e.

\[\oint \tau \times \ell T’ = \oint (\tau \times \ell T)’=0.\]

$\square$

The statement about the area vector implies for the case $n=2$ that $\gamma$ and $\eta$ enclose the same area:

\[\frac{1}{2}\oint \mbox{det}(\gamma, \gamma’) = \frac{1}{2}\oint \mbox{det}(\eta,\eta’).\]

 

Darboux Transforms of Plane Curves

Leave a reply

Again we consider curves in in the real plane. Last time we regarded the real plane as a subset of the real projective plane. This time we want to regard it as a complex line, i.e. a \(1\)-dimensional complex vector space,  and hence as a part of the Riemann sphere \(\overline{\mathbb{C}}=\mathbb{C}\cup\{\infty\}\).  The reason is that we are interested in Darboux transforms of plane curves.

In the smooth world two arc length parametrized curves \(\gamma\) and \(\eta\) are Darboux tranforms of each other if the curve \(T := \gamma-\eta\)

  1. lies on a circle of radius \(l\),
  2. is not constant.

The second condition simply prevents that one curve is just a translation of the other. The smooth definition directly translates to the discrete world. In the following we will call \(l\) the rodlength.

Definition (Discrete Euclidean Darboux Transform). Let \(\gamma\) and \(\eta\) be two discrete plane curves with the same number of vertices and such that corresponding edges have equal length. Then \(\gamma\) and \(\eta\) are Darboux transforms of each other if its difference \(T=\gamma-\eta\) lies on a circle of radius \(l\) and is not constant.

Let \(\gamma, \gamma_+, \eta\) be given. The subscript \(+\) shall be thought of as a shift by \(1\) later. We want to construct \(\eta_+\). If we look at the possible configurations we see that there exist two distinct points, that satisfy the first condition. Exactly one of both satisfies also the second condition. The construction of a so called Darboux butterfly is shown in the following picture.

darboux_construction

Hence if we start with a discrete curve \(\gamma\) and an arbitrary point \(\eta_0\) we can successively construct a Darboux transform that starts at \(\eta_0\).

Now, if we treat the real plane as complex line, then both conditions can be parsed in just one. Therefore we must first introduce the cross ratio, which is not defined on \(\mathbb C\), but on the Riemann sphere \(\overline{\mathbb{C}}\). This will become clear when we look at its

Definition (Cross Ratio). Let \(z,u,v,w\in\overline{\mathbb{C}}\) be distinct points. The cross ratio \(\{z,u,v,w\}\) of the four points is defined as follows\[\{z,u,v,w\}:=\frac{(u-v)(w-z)}{(z-u)(v-w)}.\]

It has some properties that are quiet interesting for our purpose, but first the following

Definition (Moebius transformation). A Moebius transformation is a map \(f\colon \overline{\mathbb{C}}\to \overline{\mathbb{C}}\) of the form\[ z \mapsto \frac{az+b}{cz+d},\quad ad-bc\not=0, \, a,b,c,d\in \mathbb{C}.\]Here we set\[f(\infty)=\frac{a}{c},\quad f(-\frac{d}{c})=\infty.\]

As Euclidean geometry is geometry that is invariant under Euclidean transformations, i.e. essentially translations and rotations, Moebius geometry is geometry that is invariant under Moebius transformations, i.e. essentially translations, stretch rotations and inversions in circles.

We shall list some properties here: Moebius transformations

  • build a group (composition of functions as multiplication)
  • are orientation preserving
  • can be decomposed into translations, stretch rotations and inversions
  • map circles to lines or circles
  • are uniquely determined by its values at three different points
  • different from the identity have exactly one or two fixed points

Note: With Moebius geometric eyes one cannot distinguish between straight lines and circles anymore. They can be mapped on each other by a Moebius transformation. Hence, we will simply speak only of (generalized) circles from now on – in this context a straight line is seen as a circle of infinite radius.

Here is a video to get an impression what a Moebius transformation can do. It shows quiet well what is going on.

Let’s come back to the cross ratio. The cross ratio is a Moebius geometric invariant, i.e. if \(f\) denotes a Moebius transformation, then \[\{z,u,v,w\}=\{f(z),f(u),f(v),f(w)\},\quad \forall z,u,v,w \in \overline{\mathbb{C}}.\]

We immediately obtain two more properties of the cross ratio:

  • \(\{z,u,v,w\}\in\mathbb{R}\) if and only if the four points lie on a circle (or a line)
  • \(\{z,u,v,w\}<0\) if and only if the four points are in successive order

Now let us consider the following map. For three given points \(u,v,w \in \mathbb{C}\) we define a map as follows\[z\mapsto \{u,v,z,w\}.\] This is a Moebius transformation and maps the circumcircle of the three points to the real line. In particular:\[ u \to 1,\, v \to 0,\, w \to \infty.\]

As a Moebius transformation it is in particular bijective and hence for every given \(\delta\in\overline{\mathbb{C}}\) we can find a unique \(z_\delta \in\overline{\mathbb{C}}\) such that\[\{u,v,z_\delta,w\}=\delta.\]

This is interesting for us since we have to solve exactly such a problem in the Darboux transform construction: We know the cross ratio of the points \(\gamma,\gamma_+,\eta_+,\eta\). You can easily convince yourself that the absolute value of the cross ratio has to be equal to \(\frac{l^2}{s^2}\), where \(s\) denotes the length of the edge between \(\gamma_+-\gamma\). Further we know by construction that the points \(\gamma,\gamma_+,\eta_+,\eta\) lie on a common circle and hence the cross ratio has to be real – that specifies two points on the circle. Finally, we know that the points are not in cyclic order on this circle, i.e. the cross ratio has to be positive. Altogether we see that \(\eta\) and \(\gamma\) are Darboux transforms of each other with rodlength \(l\) if and only if\[ \{\gamma,\gamma_+,\eta_+,\eta\}=\frac{l^2}{s^2},\quad s=|\gamma_+-\gamma|.\]

The notion of a Darboux transform can be generalized by allowing complex rodlengths.

Definition (Discrete generalized Darboux Transform). Let \(\gamma\) and \(\eta\) be two discrete plane curves with the same number of vertices such that corresponding edges have equal lengths \[s=|\gamma_+-\gamma|=|\eta_+-\eta|.\] Then \(\gamma\) and \(\eta\) are Darboux transforms of each other with parameter \(l\in\mathbb{C}\) if\[\{\gamma,\gamma_+,\eta_+,\eta\}=\frac{l^2}{s^2}.\]

One can check that the map \(f\) defined by \(\{u,v,f(z),z\}=\delta\) is a Moebius transformation. Hence we can construct Darboux transform to a given discrete curve \(\gamma\) by successively applying Moebius transformations that sit on the edges of \(\gamma\). To construct the transformations explicitly we will slightly change our point of view once more. The point is that a Moebius transformation can be regarded as a complex \(2\times2\)-matrix, what will simplify the implementation. How does this work?

The Riemann sphere can be identified with the complex projective line \(\mathbb{CP}^1\) by the following map\[ \mathbb{CP}^1 \ni \begin{bmatrix}z_1\\z_2\end{bmatrix} \longleftrightarrow \frac{z_1}{z_2} \in \overline{\mathbb{C}}.\] The coordinates one gets under this identification are refered to as homogeneous coordinates, which we will denote by capital letters from now on. Under this identification, a Moebius transformations is then given by an invertible complex \(2\times 2\) matrix:\[\left(z\mapsto\frac{az+b}{cz+d}\right) \longleftrightarrow \left( \begin{bmatrix} z_1 \\ z_2\end{bmatrix} \mapsto \begin{bmatrix}\begin{pmatrix} a & b \\ c & d \end{pmatrix}\begin{pmatrix}z_1\\ z_2\end{pmatrix}\end{bmatrix}\right).\] In fact, this is a group isomorphism between the group of Moebius transformations and the projective special linear group \(PSL(2,\mathbb C)=SL(2,\mathbb C)/_{\{\pm Id\}}\).

For given \(\delta\in\mathbb{C}\) we search for the unique Moebius transformation \(f\) that satisfies the equation\[\{\gamma,\gamma_+,f(\eta),\eta\}=\delta.\] The corresponding matrix is easily given in terms of the homogeneous coordinates \[\gamma=[\Gamma],\quad \gamma_+=[\Gamma_+],\quad\eta=[\text{H}].\]

Claim: The Moebius transformation \(f\) is given by the matrix \(A\) determined by the following equations:\[ A\Gamma=\Gamma, \quad A\Gamma_+= \lambda\Gamma_+,\]where\[\delta=\frac{1}{1-\lambda}.\]

To see this, first let us check how the cross ratio looks in homogeneous coordinates: \begin{align*}\left\{Z,U,V,W\right\}&=\left\{\frac{z_1}{z_2},\frac{u_1}{u_2},\frac{v_1}{v_2},\frac{w_1}{w_2}\right\}\\&=\frac{(\frac{u_1}{u_2}-\frac{v_1}{v_2})(\frac{w_1}{w_2}-\frac{z_1}{z_2})}{(\frac{z_1}{z_2}-\frac{u_1}{u_2})(\frac{v_1}{v_2}-\frac{w_1}{w_2})}\\&=\frac{(u_1v_2-v_1u_2)(w_1z_2-z_1w_2)}{(z_1u_2-u_1z_2)(v_1w_2-w_1v_2)}\\&=\frac{\det(U,V)\det(W,Z)}{\det(Z,U)\det(V,W)}.\end{align*}

Since \(\Gamma\) and \(\Gamma_+\) are linearly independent they build a basis of \(\mathbb{C}^2\)and \(A\) can be written as follows:\[ A= \tfrac{1}{\det(\Gamma,\Gamma_+)}\left(\det(.,\Gamma_+)\Gamma+\lambda\det(\Gamma,.)\Gamma_+\right).\]Now let us plug this into the equation to get the right \(\lambda\). We find \[\delta= \{\Gamma,\Gamma_+,A\text{H}, \text{H}\}=\frac{\det(\Gamma_+,A\text{H})\det(\text{H},\Gamma)}{\det(\Gamma,\Gamma_+)\det(A\text{H},\text{H})}=\frac{1}{1-\lambda}.\]

Homework. Write a plugin DarbouxTransformationPlugin that displays the Darboux transform of a given discrete curve to a given initial value. The initial value shall be movable. Exclude all calculations to a class DarbouxTransformationUtility that provides static methods. It shall be able to calculate for a given \(\delta\in\mathbb{C}\) the Moebius transformation from one vertex to another and to return the Darboux transform for given curve and initial point.

DarbouxTransform

Above a picture how this finally can look like. Usually a Darboux transform of a curve is not closed. This happens only at some points. To get this picture I had to play around a while. The thin lines connect the corresponding points of \(\gamma\) and \(\eta\). Even if not drawn one can see their envelope – it’s a tractrix.

Getting started

Leave a reply

Eclipse

During the whole course we will work with Eclipse. It can be downloaded from the  Eclipse website and is easily installed at home. In general Eclipse is quiet well documented – see the documentation.

For the communication we will use Subversive – a subversion team provider – which can be installed from the Eclipse project update sites. See here for installation instructions.

At the university different versions of Eclipse with installed Subversion are found under /net/MathVis/. We will use Eclipse Juno. Start it with the command

/net/MathVis/eclipse_juno_java_linux64bit_with_subversive/eclipse

in the terminal. Note: the default version installed at TU is also Juno but without Subversion. Make sure you start the correct one.

SVN-Repositories 

For the communication we will use subversion-server of the university. This is also the place where the repositories of jTEM and jReality lie. The server addresses are

TODO 1: Start Eclipse, open the SVN Repository Exploring perspective, and create a new Repository Location for jTEM. Check out the following projects:

  • beans
  • function
  • java2d
  • java2dx
  • jrworkspace
  • mfc
  • modelling
  • numericalMethods 

The exercises shall be stored at the course-repository which lies at the following address:

http://fs.math.tu-berlin.de:8000/svn/MathVis/SS13

The username and password is sent to you by mail. You can check it e.g. via the terminal with pine.

TODO 2: Switch in Eclipse to the Java Perspective and create a new project. The project name shall be of the form “accountname_yourname”. Create a package with the name “exercise” in your project and share the project into the course-repository. You”ll find the command in the team-menu (right-click on project folder).

Java2dViewer 

To visualize plane geometries we will use the Viewer2D from java2d in combination with jrworkspace, which with its plugin system is also an important ingredient of jReality. The result is the Java2dViewer, which can be found in the plugin package of java2dx.

How the Java2dViewer is used is demonstrated in the main-method of the class SubdividedPolygonPlugin. The class can be found in the discretePlaneCurves project, which lies in the course-repository and will be the basis for what we will do in the beginning of this course.

TODO 3: Check out the project discretePlaneCurves from the course-repository and run the SubdividedPolygonPlugin.

The whole system is based on plugins, which can be registered at the viewer. If the plugin extends View2DShrinkPanelPlugin a panel appears (if not specified differently) in the right slot of the viewer.

The most important method of such a plugin is the install method, which makes a communication between different plugins possible. The argument of this method, the Controller, knows all the available plugins and can be asked for them.

Typically this looks as follows:

private Viewer2D viewer= null;
private SubdividedPolygon2D polygon= null;

…

public void install(Controller c) throws Exception {
viewer = c.getPlugin(Java2DView.class).getViewer2D();
polygon = c.getPlugin(SubdividedPolygonPlugin.class)
.getSubdividedPolygon();
…
super.install(c);
}

So, e.g, the DualPolygonPlugin can get the polygon from the SubdividedPolygonPlugin and generate the corresponding dual curve. But what is a dual curve? How does it look like?

TODO 4: Create a class with name DualCurveViewer in the exercise-package of your project. Its main-method shall initialize a Java2dViewer, register the DualPolygonPlugin, and start the viewer. Hint: The SubdividedPolygonPlugin has a main-method that starts a viewer. Run the application and play around a while. If everything is correct, commit the changes to the repository.

In order to produce nice pictures the appearance of the curves can be changed and the result can be exported as pdf. The following pictures show two examples.

dualprojectivecurve1 dualprojectivecurve2

If one really wants to understand what is going on, we need a bit more mathematical background.

Dual Curves

If we start with a smooth 1-parameter family of lines \(L\) in the plane, then there is a smooth curve \(\gamma\) such that \(\gamma\) is tangent to each curve in the family at some point – this curve \(\gamma\) is called the envelope of \(L\). The whole story directly translates to the discrete world. If you have a sequence of lines in the plane \(L\), then there corresponds a discrete curve \(\gamma\) to it. The construction of \(\gamma\) is elementary: two successive lines have an intersection. This gives a sequence of points, i.e. a discrete curve.

But wait, where do two parallel lines intersect? Right, they do not intersect in \(\mathbb{R}^2\), but in an infinitely far “ideal” point. If want to make this precise, we have to speak about the real projective plane. Here every pair of distinct lines intersects in exactly one point. We will give a short impression. For a serious treatment see the literature. There are lots of books on this subject. I recommend the lecture notes of Nigel Hitchin on projective geometry and quadrics, which are free available on his homepage http://people.maths.ox.ac.uk/hitchin/.

Real Projective Space. The \(n\)-dimensional real projective space consists of all (unoriented) lines through the origin of a \(n+1\)-dimensional real vector space \(V\). To make this more rigorous, introduce an equivalence relation \(\sim\) on \( V_0:= V\setminus\{0\}\) as follows\[ x\sim y:\Leftrightarrow x= \lambda y ,\quad 0\not=\lambda\in\mathbb{R}.\]

We denote the equivalence class of a vector \(x\) by \([x]\). The \(n\)-dimensional real projective space \(P(V)\) is then the quotient space with respect to the defined equivalence relation:\[ P(V)= V_0/_\sim.\]

If \(V\) is 2-dimensional we call \(P(V)\) a projective line. If \(V\) is 3-dimensional we call it a projective plane.

Curves in the Projective Plane. For now we are only interested in the projective plane \(\mathbb{RP}^2= P(\mathbb{R}^3)\). Each plane \(U\subset\mathbb{R}^3\) in \(\mathbb{R}^3\) can be identified with \(\mathbb{R}^2\). If \(U\) does not contain the origin, each point in \(U\) can be identified with a point in \(\mathbb{RP}^2\) by \(x \mapsto [x]\). The points in \(\mathbb{RP}^2\) which are not obtained this way are exactly the vectors that are parallel to \(U\). This is a 2-dimensional subspace of \(\mathbb{R}^3\) – the projectivization of which is a real projective line. Hence, we can consider the real projective plane as the union of \(\mathbb{R}^2\) with a real projective line \(\mathbb{RP}^1\) – the “ideal line”:\[ \mathbb{RP}^2= \mathbb{R}^2\cup \mathbb{RP}^1.\]

In this sense each plane curve \(\gamma=(\gamma_1,\gamma_2)\) lifts to a projective one. If we choose \(U= \{x\in\mathbb{R}^3\mid x_3=1\}\) then the map is simply given by \[ \gamma \mapsto \Gamma = [\gamma_1,\gamma_2,1]. \]

Opposite, if we have a projective curve \(\Gamma=[\Gamma_1,\Gamma_2,\Gamma_3]\) that does not pass the ideal line, i.e. \(\Gamma_3\not= 0\), then we can get corresponding curve in \(\mathbb{R}^2\) by normalizing the last component to \(1\):\[ \Gamma \mapsto \gamma= (\Gamma_1/\Gamma_3,\Gamma_2/\Gamma_3).\]

If \(\Gamma\) is a general projective curve, we call the part which does not intersect the ideal line the finite part of \(\Gamma\).

Curves of lines. What does this have to do with families of lines in \(\mathbb{R}^2\)? A line \(L\) in the real plane can given by an equation\[ L_{(a,b,c)}=\{(x,y)\in \mathbb{R}^2 \mid ax+by-c=0\}\quad a,b,c\in \mathbb{R}.\]

So we see that lines are essentially given by vectors in \(\mathbb{R}^3\). But the equation can be multiplied by an arbitrary non-zero scalar while the line does not change. Thus the line corresponds to a point in the projective plane.

How the line can be recovered from that point \([a,b,-c]\in\mathbb{RP}^2\)? Consider the linear form \[ \eta_{(a,b,c)} (x,y,z) = ax+by-cz. \]

The projectivization of its kernel is a projective line the finite part of which is exactly \(L_{(a,b,c)}\).

So we have seen that plane curves and smooth families of lines both can be regarded as curves in the projective plane.

Polarity. Let \(Q\) be an indefinite non-degenerate quadratic form on \(\mathbb{R}^3\). By Sylvester’s law of inertia every such form on \(\mathbb{R}^3\) arises from a standard form by a change of basis. We can assume without loss of generality that the form is represented by the matrix the following matrix: \[Q=\begin{pmatrix} 1&0&0\\ 0&1&0\\ 0&0&-1 \end{pmatrix}.\]

The quadric \(\mathbf Q \subset \mathbb{RP}^n\) is defined as the zero set of \(Q\), i.e.\[ \mathbf Q= \{[x]\in \mathbb{RP}^2 \mid Q(x,x)=0\}.\]

Note, that the zero set is also well defined in the projective setting. The intersection with the plane \(\{z=1\}\) is just a round circle. If one instead intersects it with other planes one gets the usual plane conic sections as shown in the picture below.

Conic_sections_with_plane

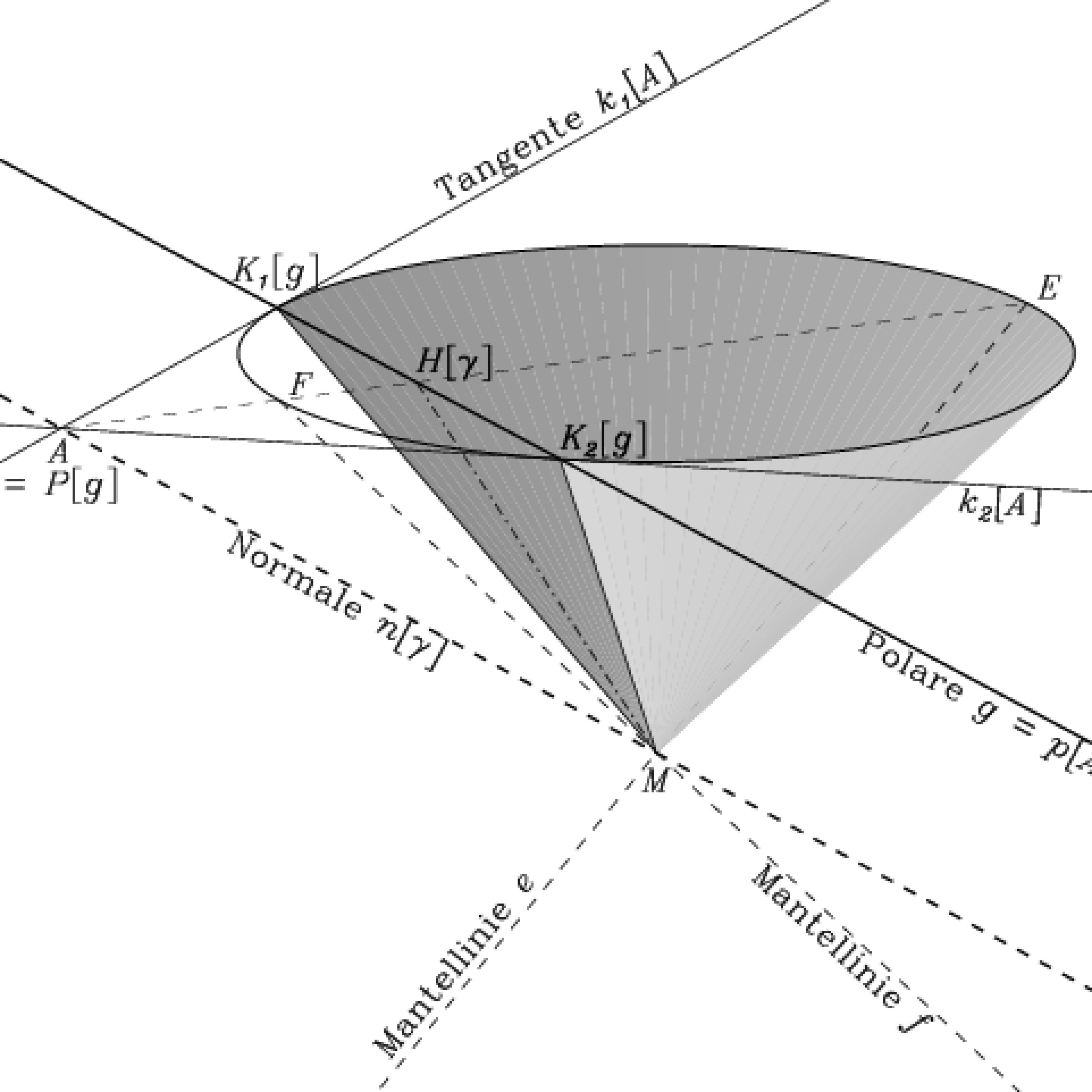
With \(Q\) we get an isomorphism from \(\mathbb{R}^3\) to \(\mathbb{R}^3\). It is given by the following map\[ (a,b,c)\mapsto (a,b,-c).\]

Under this map the point \((a,b,c)\) is identified with \(L_{(a,b,c)}\), called the polar of the point. The correspondence has also a nice geometric construction as shown in the next picture (taken from here).

polarity

Using this duality we get for each projective curve \(\gamma\) a dual projective curve \(\Gamma\).

The dual curve \(\Gamma\) of a curve \(\gamma\) in \(\mathbb{R}^2\) is defined as the envelope of the line field corresponding to the dual curve of the projective curve induced by \(\gamma\). Hopefully, this won’t lead to confusion.

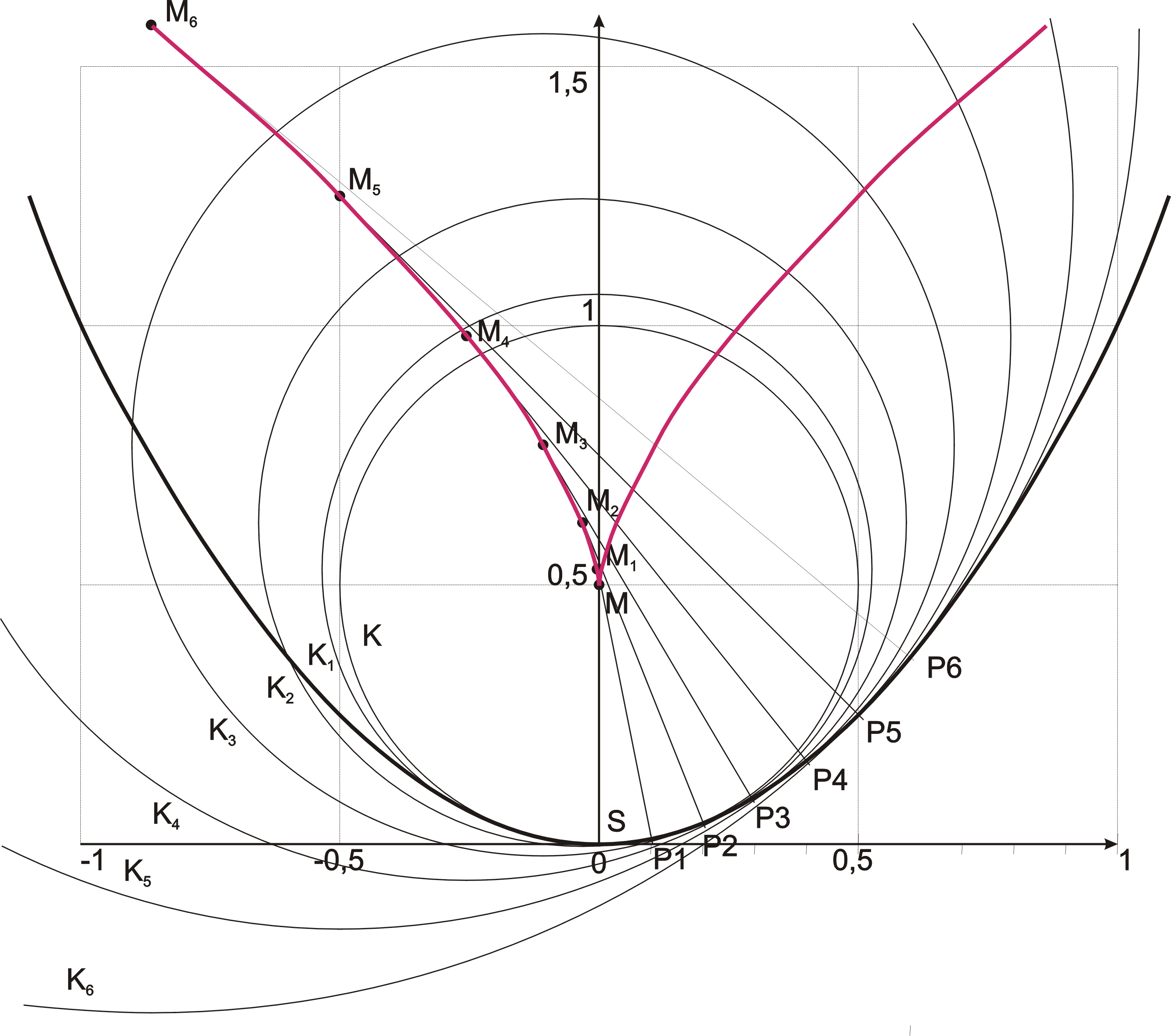
The curve does not have to stay in the finite part, but can also pass the ideal line as shown in the picture below.

multiple_components

The evolute of a curve

Smooth case. Let \(\gamma\) be a plane curve. The evolute of \(\gamma\) is defined as the envelope of the normal field of \(\gamma\). It can be shown that the evolute \(\hat\gamma\) is given by \[ \hat\gamma= \gamma+\tfrac{1}{\kappa}N,\] where \(N\) denotes the normal field and \(\kappa\) the curvature of \(\gamma\). If \(\gamma\) was arclength parametrized \(\kappa\) is given by\[ T^\prime= \kappa N. \]

The osculating circle of \(\gamma\) is the circle that touches \(\gamma\) of second order. Its center \(c_\kappa\) is called the center of curvature. Its radius \(R\) and \(\kappa\) are related by\[ R= \left|\tfrac{1}{\kappa}\right|. \] In other words: The evolute is the trace of the center of curvature.

constructionevolute

Discrete case. While it is clear what the normal field is in the smooth case, there are different possible choices of normal directions in the discrete case. It is even not clear whether they sit at vertices or on the edges, but there are good possible choices.

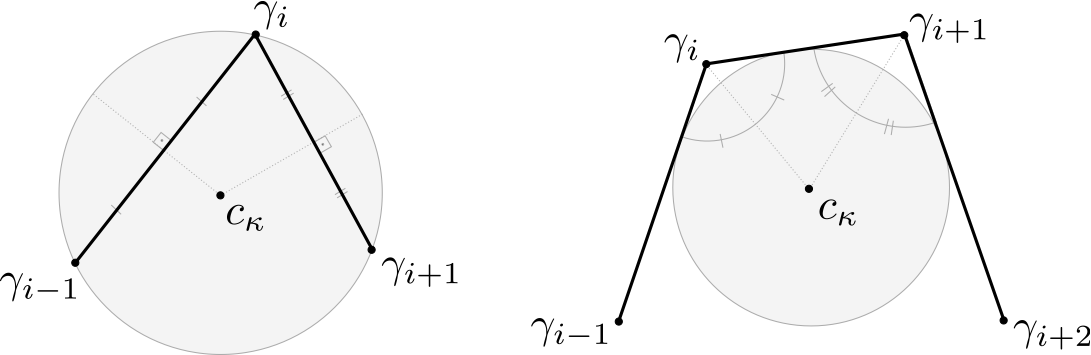
discretecenterofcurvature

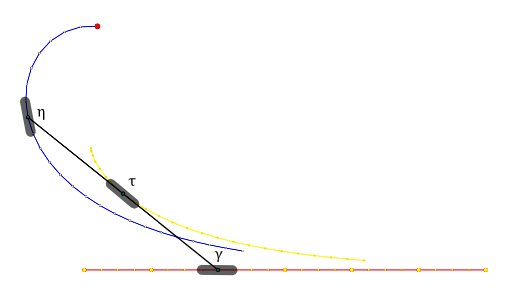
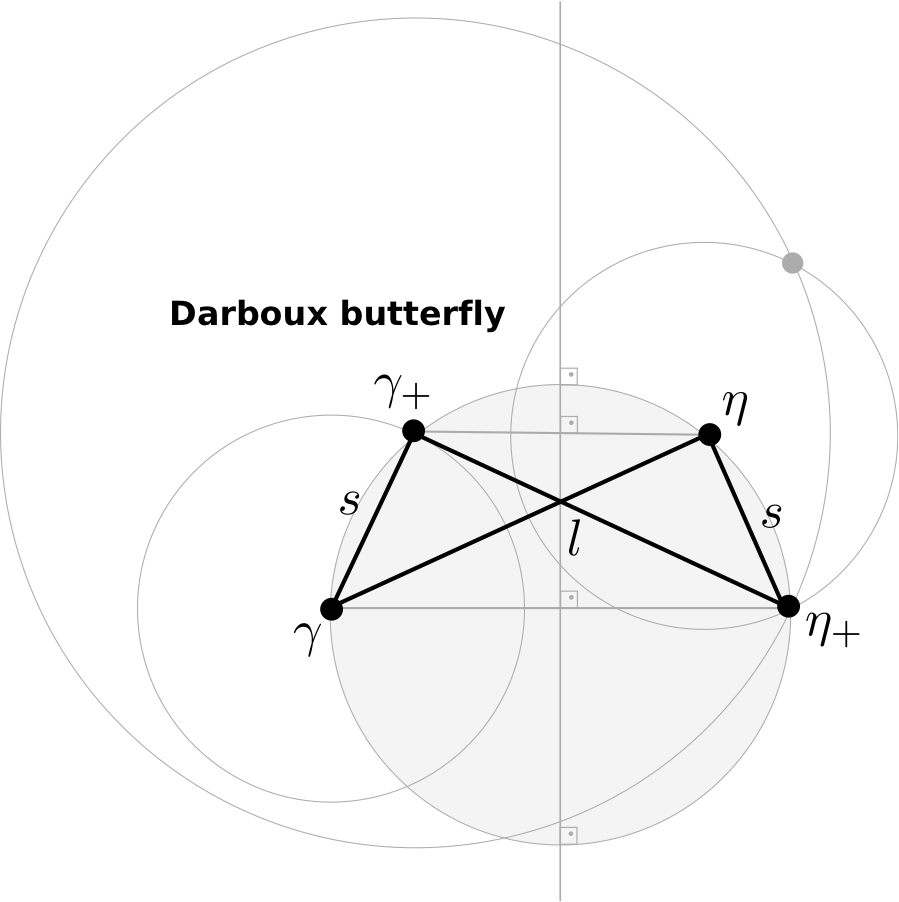
Possibility 1: Define the normal spaces at edges. Here the most obvious choice is to take the edge bisector (see here e.g.). The edge bisectors of two successive edges meat in the circumcenter of the triangle that is determined by the two involved edges.

Hence one possibility of a discrete evolute is to define it as the sequence of circumcenters of three successive vertices.

In fact, we can easily translate that into the projective curve setting, i.e. we can specify the normal field by a projective curve. Drawing the envelope yields nice results. Below you find two examples of evolutes defined using edge bisectors.

evolute2 evolute1

Possibility 2: Define the normal spaces at vertices. Here the angle bisectors that cross the discrete curve seem to be a good choice. The angle bisectors of two successive vertices meat in the center of a circle that touches the three edges that incident with the vertices – another osculating circle.

Homework: Implement both definitions of a discrete evolute, i.e. write a plugin that can switch between the two definitions. Use for it the DualPolygon2D class, which allows you to specify a projective curve, which interprets a dual projective curve as a curve of lines in the plane. The envelope is drawn automatically.