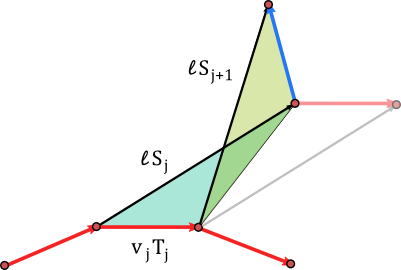
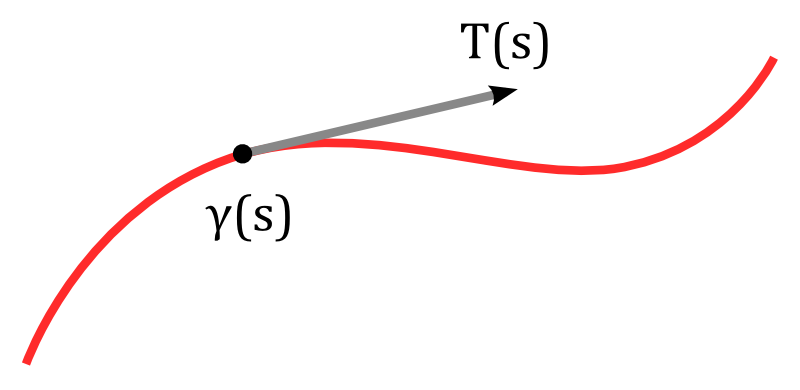
Let us investigate the tracks traced out by the wheels of a moving bicycle during some time interval $[a,b]$. We denote the path of the (center of the) rear wheel by $\tau$ and the path of the front wheel by $\gamma$. If $\ell$ is the distance between the rear and the front wheel then at each time $t$ the direction of the bicycle is given by a unit vector $T(t)$ such that
\[\gamma=\tau+\ell\, T.\]
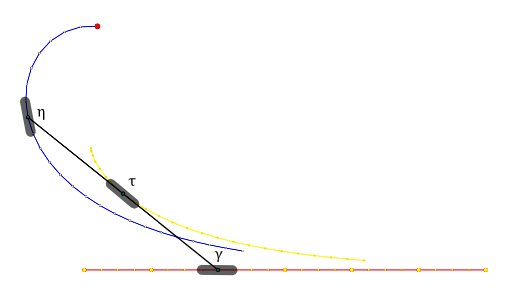
In the picture below the front wheel $\gamma$ moves on a straight line. The resulting path of the rear wheel is called the tractrix curve and has been investigated already in 1676 by Isaac Newton and in 1692 by Christian Huygens.
Assuming that the rear wheel rolls without sliding it must move in the direction of $T$: There is a function $\rho: [a,b] \to \mathbb{R}$ such that
\[\tau’=\rho T.\]
Suppose the bicycle is prolonged in the rear direction by a rod. We assume that the tip of the rod has distance $\ell$ to the center of the rear wheel (only projections to the horizontal plane are considered here). Then the position $\eta(t)$ of the tip of the rod is given as
\[\eta=\tau-\ell T.\]
The rotation speed $\omega(t)$ of the bicycle is defined via
\[T’=\omega JT.\]
From
\begin{align*}\gamma’ &= \rho’ T+\ell \omega JT \\\\ \eta’ &= \rho’ T-\ell \omega JT \end{align*}
it is easy to see that the velocity vector $\eta’$ of the back end is equal in magnitude to the speed $\gamma’$ of the front wheel:
\[|\eta’|^2=\rho’^2+\omega^2=|\gamma’|^2.\]
Moreover, if we were to install another wheel at the rear end that also rolls without sliding it would have to make the same angle (though opposite in direction) with the bicycle as the front wheel. Such a bicycle (omitting the middle wheel) has in fact been built, even though I have to admit that the video does not look convincing.
On the other hand, cars with four-wheel steering are manufactured in some variety. The motion of cars with four wheels is more difficult to analyze, but to some approximation we might assume also here that the center $\tau$ of the rear axis moves towards the center $\gamma$ of the front axis. The right picture below shows a DAF MC-139 prototype from 1940 (yes, it has two driver seats). The model in the left picture even has the middle wheels (showing the tractrix) and a video can be found here.

Let us condense all this into a mathematical
Definition: Let $\tau: [a,b]\to \mathbb{R}^n$ be a path and suppose there are $T:[a,b] \to\mathbb{R}^n$ of unit length $|T|=1$ and $\rho: [a,b] \to \mathbb{R}$ such that $\tau’=\rho T$. Then for every $\ell\in \mathbb{R}$ the path $\tau$ is called a tractrix of the path $\gamma:=\tau+\ell\,T$. Furthermore $\eta:=\tau-\ell\,T$ is called a Darboux transform of $\gamma$.
It is easy to see that in the above situation $\tau$ is a tractrix also of $\eta$ and $\gamma$ also is a Darboux transform of $\eta$. The paths $\gamma$ and $\eta$ always have the same length. Note that if $\gamma$ is regular then so is $\eta$ and if $\gamma$ is parametrized by arclength then the same holds for $\eta$.
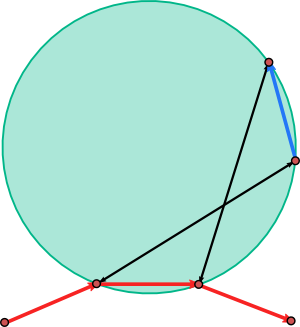
We can apply similar definitions in the case of closed curves by assuming that $\tau$, $T$ and $\rho$ are periodic functions.
Theorem: Suppose $\eta$ is a Darboux transform of a periodic path $\gamma$ in $\mathbb{R}^n$ that is parametrized by arc length. Then $\gamma$ and $\eta$ have the same length and the same total squared curvature
\[\oint |\gamma”|^2=\oint |\eta”|^2.\]
If $n=3$ then $\gamma$ and $\eta$ have the same area vector
\[\frac{1}{2}\oint \gamma \times \gamma’ = \frac{1}{2}\oint \eta \times \eta’.\]
Proof: We have
\[\gamma’=\rho T + \ell T’\]
and we may assume that $\gamma$ and $\eta$ are parametrized by arc length, i.e.
\[\rho^2+\ell^2|T’|^2=1.\]
Then
\[\gamma”=\rho’T+\rho T’+\ell T”\]
and
\[\oint \langle \gamma”,\gamma”\rangle =\oint \rho’^2 + 2\ell \langle \rho’ T +\rho T’,T”\rangle +\ell^2 |T”|^2.\]
We want to show that this expression is unchanged if we replace $\ell$ by $-\ell$, i.e.
\[\oint \langle \rho’ T +\rho T’,T”\rangle = \oint -\rho’ \langle T’,T’ \rangle – \frac{\rho}{2}\langle T’,T’\rangle’ =\oint \rho'(\rho^2-1)+\rho^2\rho’=0.\]
Here we have used $0=\langle T,T’\rangle’=\langle T’,T’\rangle+\langle T,T”\rangle$, the equation $\rho^2+\langle T’,T’\rangle =1$ and its derivative $2\rho \rho’+\langle T’,T’\rangle’=0$.
Next we look at the area vector
\[\oint \gamma \times \gamma’ = \oint (\tau+\ell T)\times (\rho T+\ell T’).\]
Again we only have to show that the coefficient of $\ell$ vanishes, i.e.
\[\oint \tau \times \ell T’ = \oint (\tau \times \ell T)’=0.\]
$\square$
The statement about the area vector implies for the case $n=2$ that $\gamma$ and $\eta$ enclose the same area:
\[\frac{1}{2}\oint \mbox{det}(\gamma, \gamma’) = \frac{1}{2}\oint \mbox{det}(\eta,\eta’).\]