A discrete function $f$ on a discrete surface is just a map
$f: V \rightarrow \mathbb{R}$.
The derivative of $f$ is the function
$df: E \rightarrow \mathbb{R}$
$df(e) = f(\textrm{end}(e))-f(\textrm{start}(e))$.
$df$ has the property
$df \circ \rho = -df$
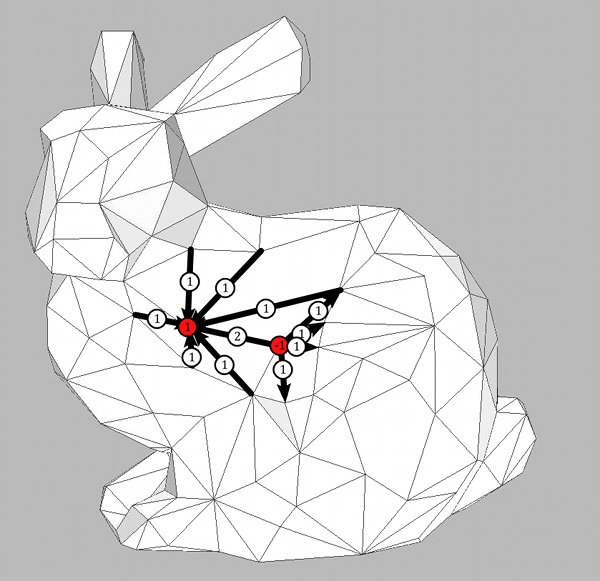
One way to visualize simple functions is to write $f(v)$ on every vertex $v$ where $f(v)\neq 0$. To visualize the derivative one can choose for each unoriented edge $\epsilon$ on which $df$ does not vanish that oriented edge $e \in \epsilon$ for which $df(e) >0$. Then one can draw $e$ as an arrow and indicate the “strength” of $df$ on $e$ by writing the number $df(e)$ on the arrow. Of course one could also choose for every $\epsilon$ an arbitrary orientation $e \in \epsilon$, draw the arrow and indicate $df(e)$ by writing the (now possibleý negative) number $df(e)$ on the arrow. The above convention has the advantage that the resulting picture almost looks like the gradient vector field of a smooth function on a smooth surface.