A path in $M$ from a vertex $i$ to a vertex $j$ is a finite sequence $(e_1, \ldots ,e_m)$ of oriented edges such that

$\textrm{end}(e_k) = \textrm{start}(e_{k+1})$

and $\textrm{start}(e_{1})=i$, $\textrm{end}(e_m) =j$.

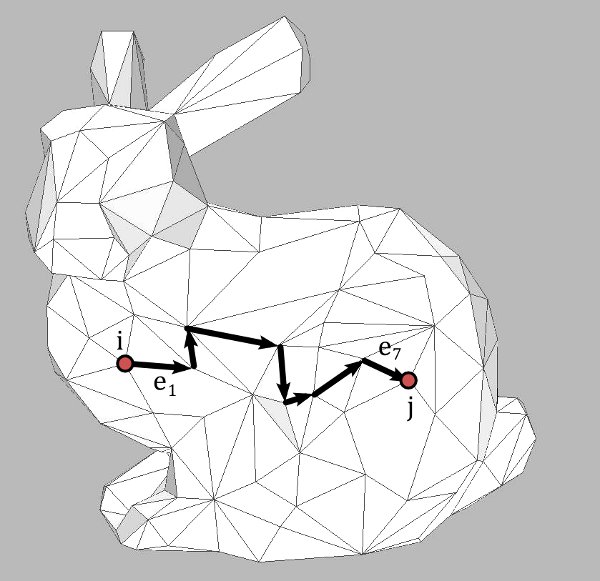A surface is called connected if for any two vertices $i,j \in V$ there is a path from $i$ to $j$. If a surface $M$ is not connected, it is not difficult to see that it nevertheless can uniquely be represented as the disjoint union of several connected surfaces (called the connected components of $M$). Usually we will assume that the surfaces we work with are connected.