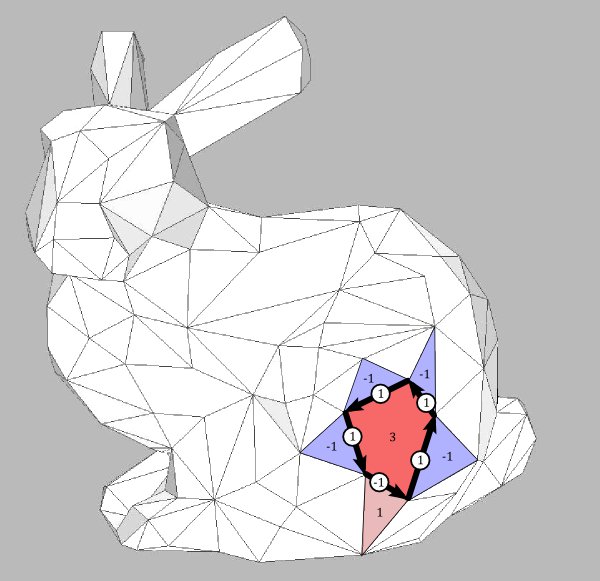
For a discrete 1-form $\omega$ we define a discrete 2-form $d\omega$, called the derivative of $\omega$:

$\displaystyle d\omega(\varphi) = \int_\varphi d\omega :=  \sum_{e \in \varphi}\omega(e)$.

The picture below illustrates this.

Recall that a 1-form $\omega$ is called exact if it is the derivative of some 0-form. $\omega$ is called closed if $d\omega =0$. It is easy to see that exact 1-forms are always closed:

$d(df)=0$.

Now that we have two maps called $d$, we sometimes distinguish them by an index. Thus

$d_0: \Omega_0(M) \rightarrow \Omega_1(M)$

$d_1: \Omega_1(M) \rightarrow \Omega_2(M)$

$d_1 \circ d_0 =0$.

The derivative of dual 0-forms provides us with a linear map

$\partial_2 : \Omega_2(M)^*=\Omega_0(M^*)\rightarrow \Omega_1(M^*)=\Omega_1(M)^*$.

Our definitions imply that $\partial_2$ is the adjoint of $d_1$:

\begin{align*}
\langle\partial f, \omega \rangle &= \sum_{e \in \hat{E}} \partial f(e) \, \omega(e) \\
&=\frac{1}{2}\sum_{e \in E} \partial f(e) \, \omega(e) \\
&=\frac{1}{2}\sum_{e \in E} (f(\textrm{left}(e))-f(\textrm{right}(e))) \, \omega(e) \\
&=\frac{1}{2}\sum_{e \in E} (f(\textrm{left}(e))-f(\textrm{left}(\rho(e)))) \, \omega(e) \\
&=\frac{1}{2}\left(\sum_{e \in E} f(\textrm{left}(e))\omega(e) -\sum_{e \in E}f(\textrm{left}(\rho(e))) \, \omega(e) \right)\\
&= \frac{1}{2}\left(\sum_{e \in E} f(\textrm{left}(e))\omega(e) -\sum_{e \in E}f(\textrm{left}(e) \, \omega(\rho(e)) \right)\\
&=\sum_{e \in E} f(\textrm{left}(e)) \omega(e)\\
&=\sum_{\varphi \in F} \sum_{e \in \varphi}f(\textrm{left}(e)) \omega(e) \\
&=\sum_{\varphi \in F} f(\varphi) \sum_{e \in \varphi}\omega(e) \\
&=\sum_{\varphi \in F}f(\varphi)d\omega(\varphi)\\
&=\langle f, d\omega \rangle.
\end{align*}