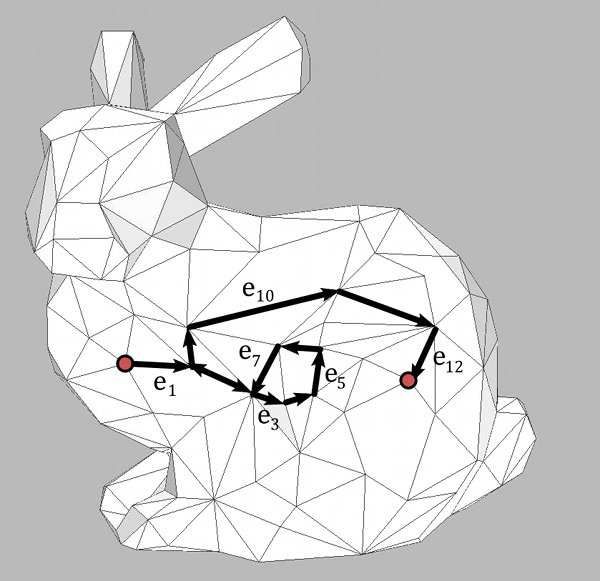
To each path $\gamma = (e_1, \ldots ,e_n)$ we can associate a dual 1-form $\hat{\gamma}$ given by
$\hat{\gamma}(e) =\#\{k\in \{1,\ldots,n\} \,|\, e=e_k\}-\#\{k\in \{1,\ldots,n\} \,|\, e=\rho(e_k)\}$.
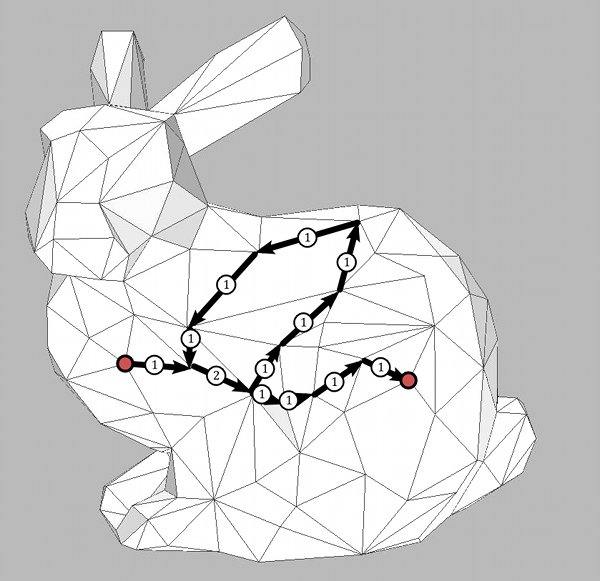
Here are two examples: The following path $\gamma$ passes through one edge $e_2=e_9$ twice:
The corresponding dual 1-form $\hat{\gamma}$ has evaluates to 2 on this edge.
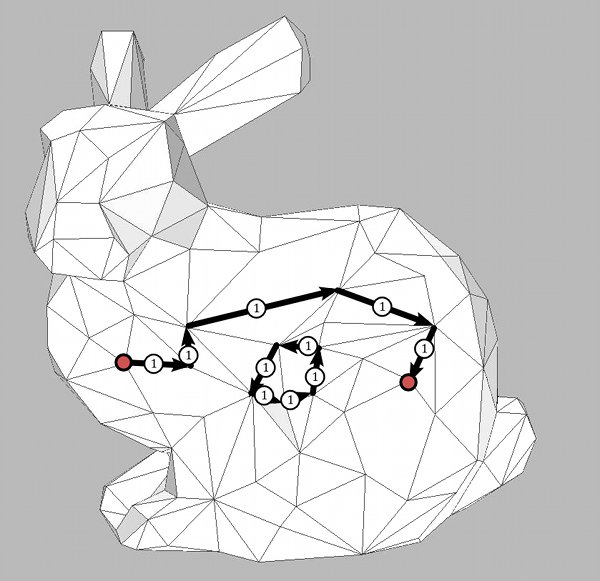
The second example contains the edges $e_2$ and $e_8=\rho(e_2)$.
In the corresponding dual 1-form these two edges cancel:
Let us calculate the derivative of the dual 1-form $\hat{\gamma}$ associated to a path $\gamma$:
\begin{align*}
d\hat{\gamma}(v) &= \sum_{e\in v} \hat{\gamma}(e)\\
&=\sum_{e\in v} (\#\{k\in \{1,\ldots,n\} \,|\, e=e_k\}-\#\{k\in \{1,\ldots,n\} \,|\, e=\rho(e_k)\})\\
&=\#\{k\in \{1,\ldots,n\} \,|\, \textrm{end}(e_k)=v\}-\#\{k\in \{1,\ldots,n\} \,|\, \textrm{start}(e_k)=v\}.
\end{align*}
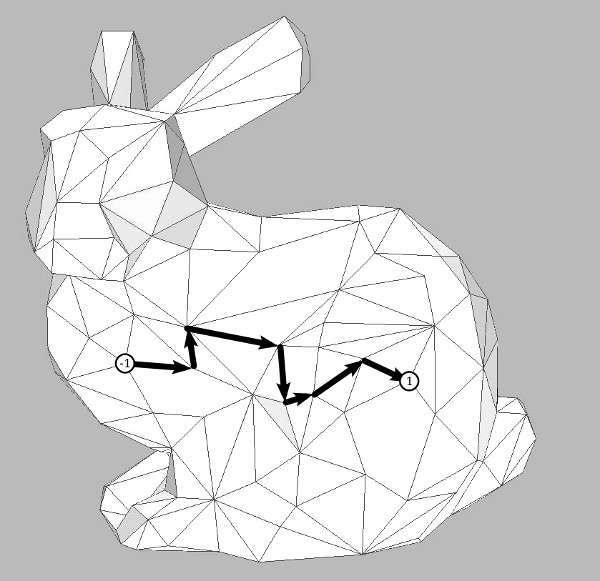
If $\gamma$ is closed, this will be zero for all vertices $v$. This is because a closed path enters any vertex as often as it leaves it. On the other hand, if $\gamma$ is not closed, the $d\hat{\gamma}$ evaluates to $1$ on the vertex $\textrm{end}(\gamma)$ to $-1$ on $\textrm{start}(\gamma)$ and to zero on all other vertices.
In particular this implies that for a closed path $\gamma$ the dual 1-form $\hat{\gamma}$ is also closed, i.e. $\partial \hat{\gamma}=0$.