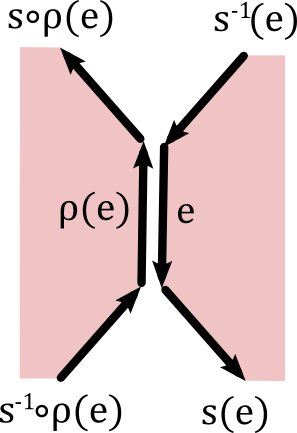
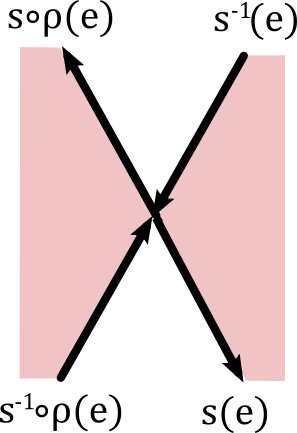
Let $M$ be a connected surface with at least four oriented edges (if there only two edges then we know we have a sphere). Suppose we have an edge $e \in E$ with

$\textrm{left}(e) \neq \textrm{right}(e)$

We want to delete $e$ and $\rho(e)$ from $E$ and define permutations $\bar{s},\bar{\rho}$ on the set

$\bar{E}=E-\{e,\rho(e)\}$

of remaining edges. We will not touch $\rho$, so

$\bar{\rho} := \rho|_{\bar{E}}$.

What about $\bar{s}$?

If all the edges are gone after the deletion (because each of them were either $e$ or $\rho(e)$) then $\{e,\rho(e)\}$ would have been a subset of $E$ invariant under both $s$ and $\rho$. Since $M$ is connected, this subset would have been the whole of $E$, contradicting our assumption that we had at least four edges.

Let us look at the case where $s^{-1}(e)$ is one of the remaining edges (the other cases are similar). Also $s\circ \rho$ is then still alive because it cannot have been equal to $\rho(e)$ (which belongs to a different face) and if it would have been $e$ it would have been equal to $s^{-1}(e)$, which we assumed is still there. If $s\circ \rho(e)$ is gone, then it must have been equal to $\rho(e)$ (since $e$ belongs to a different face). This means that $s^{-1}\circ \rho(e)$ is also gone. Nothing is then left of the face containing $\rho(e)$. We then define

$\bar{s}(s^{-1}(e)):=s(e)$.

Note that $s$ is still bijective. If on the other hand $s\circ \rho(e)$ is still available, then (by similar arguments as above) so is $s^{-1}\circ \rho(e)$ and we can we define

$\begin{align*}\bar{s}(s^{-1}(e))&:=s\circ\rho(e)\\ \bar{s}(s^{-1}\circ \rho(e))&:=s(e)\end{align*}$

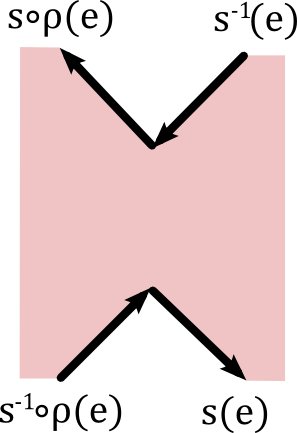In both of the above cases we end up with a new surface $\bar{M}$ (still connected) having two edges less, the same number of vertices and the number of faces has been reduced by one. We call this process “erasing” an edge.

Suppose we have an edge $e \in E$ with

$\textrm{start}(e) \neq \textrm{end}(e)$

Then a similar process as above leads to a new surface $\bar{M}$ (still connected) having two edges less, the same number of faces and the number of vertices has been reduced by one. We call this process “contracting” an edge.

When $\bar{M}$ is obtained from $M$ by erasing an edge we say that $M$ is obtained from $\bar{M}$ by “splitting a face”. Similarly we use for the opposite of “contracting an edge” the name “splitting a vertex”.

Definition: Two discrete surfaces $M,\tilde{M}$ are said to be topologically equivalent if $\tilde{M}$ can be obtained from $M$ through a sequence of erasing or deleting edges or splitting faces or vertices.

Note that two topologically equivalent surfaces have the same Euler characteristic $\#V-\#\tilde{E}+\#F$. So the genus of a surface is a topological invariant.