Painting a torus sounds like a simple task.  And, given an existing physical torus, it is simple. But if you want to paint a mathematical torus, represented by a model on the computer, then things get more difficult.  A glance at the image below may explain what I mean.

Quotient spaces. First recall the representation of the torus $T^2$ as a quotient of $\mathbb{R}^2$ by the discrete group $\Gamma$ generated by two independent translations; for simplicity assume unit translations in the $x$- and $y$-directions.  This group defines an equivalence relation on $\mathbb{R}^2$ according to $P \sim Q \leftrightarrow \exists ~\mathbf{g} \in \Gamma$ such that $P = \mathbf{g}(Q)$.  Then the set of equivalence classes wrt $\sim$ has a natural topology making it homeomorphic to $T^2$.

Fundamental domain. We choose a simply connected fundamental domain for  $\mathbb{R}^2/\Gamma$:  the half-open unit square $\mathbf{Q} := [0,1)\times [0,1)$. $\mathbf{Q}$ contains exactly one representative of each equivalence class.  We denote the map $\mathbb{R}^2 \rightarrow \mathbf{Q}$ which takes a point $P$ to its equivalent point in $\mathbf{Q}$ as $[P]$.  To obtain an embedded torus in $\mathbb{R}^3$,  apply an embedding map $e: Q \rightarrow \mathbb{R}^3$.  Notice that we can map any point in $\mathbf{R}^2$ onto the torus by the composition $P\rightarrow e([P])$.

Drawing line segments.  The paint program is designed to draw line segments on the torus.  By a line segment on the torus we  mean the image of a line segment $l(P,R)$ joining points $P, R \in \mathbb{R}^2$ under the map mentioned above, e([P])$.  Calling this a line segment on the torus, by the way implies that we are working with a flat euclidean torus which inherits its metric properties from the euclidean plane, not from $\mathbf{R}^3$.  That means that there are many different line segments joining the points $[P]$ and $[R]$ on the torus.

Assignment5. After this introduction, let’s turn to the actual application Assignment5, which you are now encouraged to try out. The boundaries of the original square are drawn as black curves on the torus.  A line segment is drawn starting at the point where the user presses on the mouse button and ending where he releases  it.  The line segment between the points  $P$ and $R$ is then $e(l(e^{-1}(P), e^{-1}(R))$.  The original coordinates of a point on the torus are available to the paint program as texture coordinates $(u,v) \in [0,1)\times [0,1)$.  As a result, no line segment that is drawn crosses over the black curves on the torus, since none of the pulled-backed line segments do.  Try painting yourself with Assignment5 to convince yourself that it’s impossible to draw a line segment that crosses a black curve. 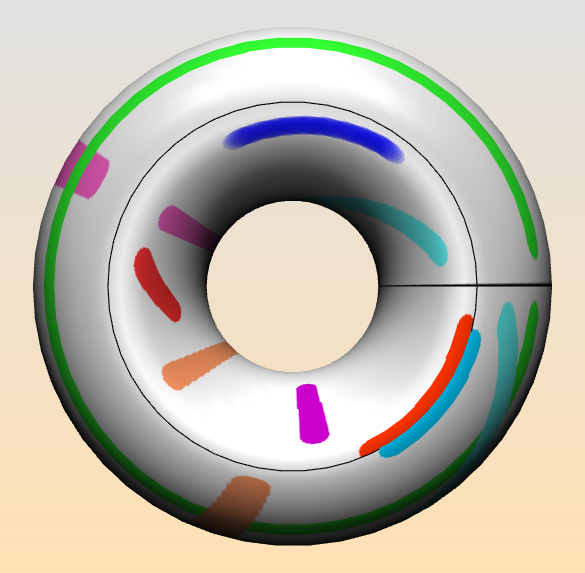Part 1. In this assignment you are asked change this behavior, so that you draw a line segment which has the same end points $P$ and $R$ on the torus, but is the shortest possible such segment (or, if there are several shortest segments, draws one of these shortest segments). One approach is to consider the universal cover of the torus, $\mathbb{R}^2$. There, each point $(x,y)$ on the torus has infinitely many equivalent points $(x+n, y+m)$ for integer $(n,m)$.   Fix $P$ and let $R$ vary over its equivalent points $\{R_(n,m)\}$.  Among these points, find the one closest to $P$ and draw the line segment joining the two points using the map $P\rightarrow e([P])$.

Part 2. There is another aspect of the paint program on the torus which is not correct.  What happens when you draw a line segment very close to, and on one side of, one of the black curves?  See in the image the parallel red and blue curves in the lower right.  You see that although the end points are correct, neither curve is fully drawn: they are too thin, and end abruptly at the black boundary. This depends on the fact that the line segments are drawn as a sequence of disks.  In the simplest case, imagine a line segment of length 0 that draws a single disk.  If the center of the disk is too close to one of the black curves, then, in the current implementation, those parts of the disk which lie on the “other” side of the black boundary from the center point, will not be drawn.  The second part of the assignment is then to modify the way that the disks are drawn so that a complete disk is drawn even if the black boundary curves intersect the disk.  (This part of the assignment is harder than the first part.) You will probably need to copy Assignment5 and the class util.Paint3DTool into your own directory.  Modify Assignment5 to use the copy of Paint3DTool you have made, and modify this copy of Paint3DTool to have the behavior described above.  I have inserted some more specific hints about how to proceed into the source code, please read the comments.