In the context of surfaces the strict analog of arclength parametrized curves is an isometric immersion
\[f: M\to \mathbb{R}^3\]
of a standard surface into $\mathbb{R}^3$. Here “isometric” means that lengths of curves and intersection angles of curves on the surface remain the same as they were on the standard surface $M$. As an example, here is an isometric immersion of an annulus in $\mathbb{R}^2$:
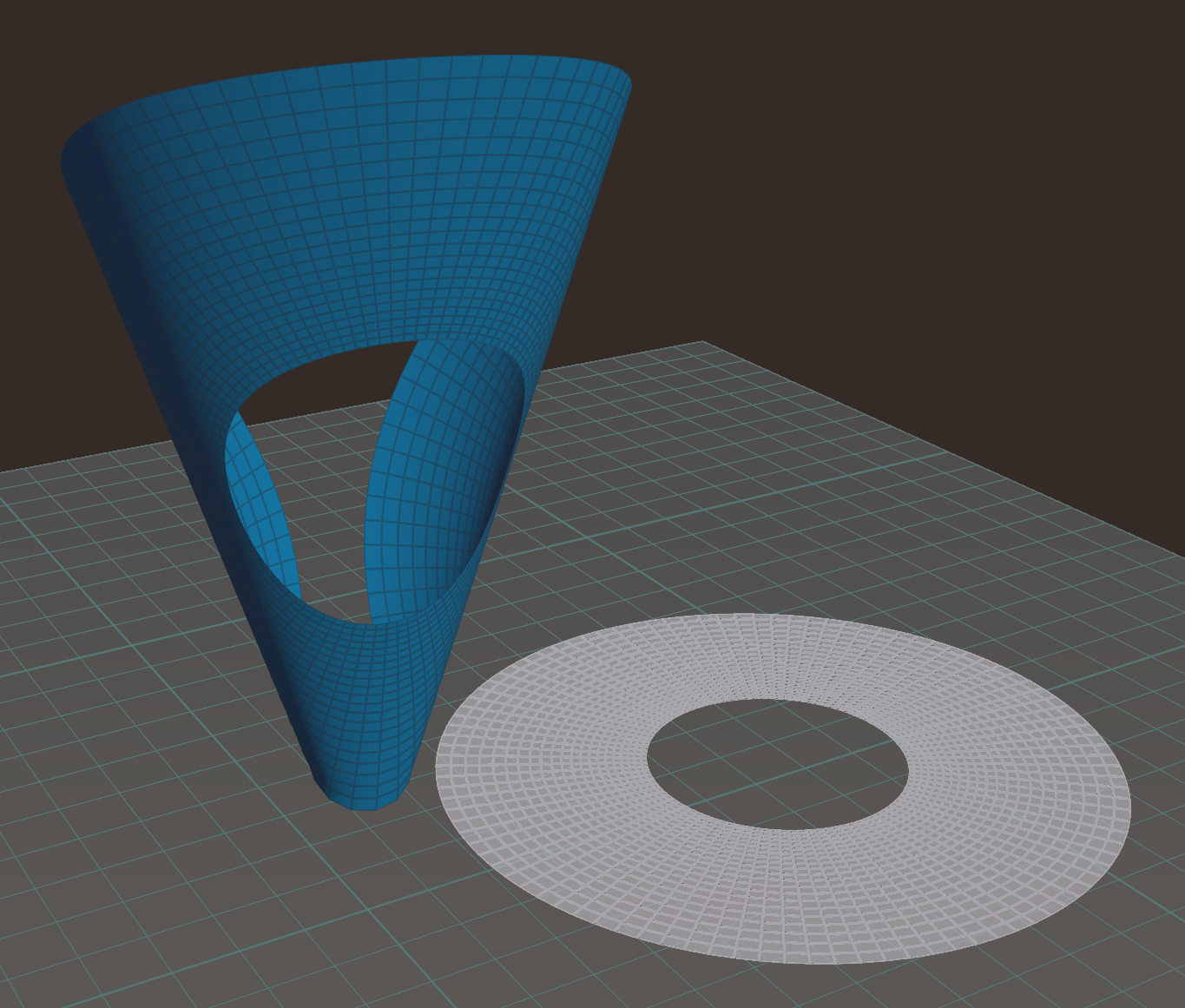
Here we used in a Point Wrangle node the following VEX code that wraps the $z,x$-plane isometrically around a cone:
#include "Math.h"
float alpha = PI/180 * ch("alpha");
float ca = cos(alpha);
float sa = sin(alpha);
float z = @P.z;
float x = @P.x;
float r = sqrt(z*z + x*x);
float phi = atan2(z,x)/ca;
@P.z = ca * r * cos(phi);
@P.x = ca * r * sin(phi);
@P.y = sa * r;
If the parameter domain is a subset $M\subset \mathbb{R}^2$, the standard coordinates of $\mathbb{R}^2$ are labeled $u,v$ and subscripts denote partial derivatives then $f$ is isometric if and only if
\begin{align*}\left|f_u\right|=\left|f_v\right|&=1 \\\\ \langle f_u,f_v\rangle &=0.\end{align*}
Very few surfaces admit such an isometric parametrizations. Also the possible isometric deformations of a given surface in $\mathbb{R}^3$ are quite limited and rigid. We therefore look at the larger class of conformal deformations, which preserve intersection angles of curves on the surface but not the length. So local features are enlarged or shrunk but not distorted.

A parametrization $f$ defined on a domain $M\subset \mathbb{R}^2$ is conformal if and only if the exists local scalings $e^\phi$ defined by a function $\phi: M \to \mathbb{R}$ such that
\begin{align*}\left|f_u\right|=\left|f_v\right|&=e^\phi \\\\ \langle f_u,f_v\rangle &=0.\end{align*}
For many applications (including numerical computations) it is desirable that the triangles of a simplicial surface are as equilateral as possible. Similarly often the quadrilaterals of a quadrilateral mesh should preferably as square-shaped as possible. Conformal deformations have the pleasant feature that they do not deteriorate the quality of the mesh (when measured in this sense).
