Plateau problem

Let $\mathrm{\Sigma }=(V,E,F)$ be a triangulated surface (with boundary). A realization of the surface in ${\mathbb{R}}^3$ is given by a map $p:V\to {\mathbb{R}}^3$ such that $p_i,p_j,p_k$ form a non degenerated triangle in ${\mathbb{R}}^3$ for all $\{i,j,k\}\in \mathrm{\Sigma }$, (i.e. $p_i,p_j,p_k$ do not lie on a line). Some problems, like the plateau problem do not depend on the position of the vertices in the space, but only on the length of the edges:
$$l_{ij}=l_{ji}=|e_{ji}|i,j\in E.$$
If we have a realization of the surface in ${\mathbb{R}}^3$ there holds: $l_{ij}=l_{ji}=|p_i-p_j|$ and the edge length’s satisfy the triangle inequalities:
$$\text{For }\{i,j,k\}\in F\Rightarrow \{\begin{array}{c}{l}_{ij}<l_{jk}+l_{ki},\\ l_{ki}<l_{ij}+l_{jk},\\ l_{jk}<l_{ki}+l_{ij}.\end{array}$$

Definition: A metric on a triangulated surface assigns  a length to each oriented edge such that the triangle inequalities are satisfied.

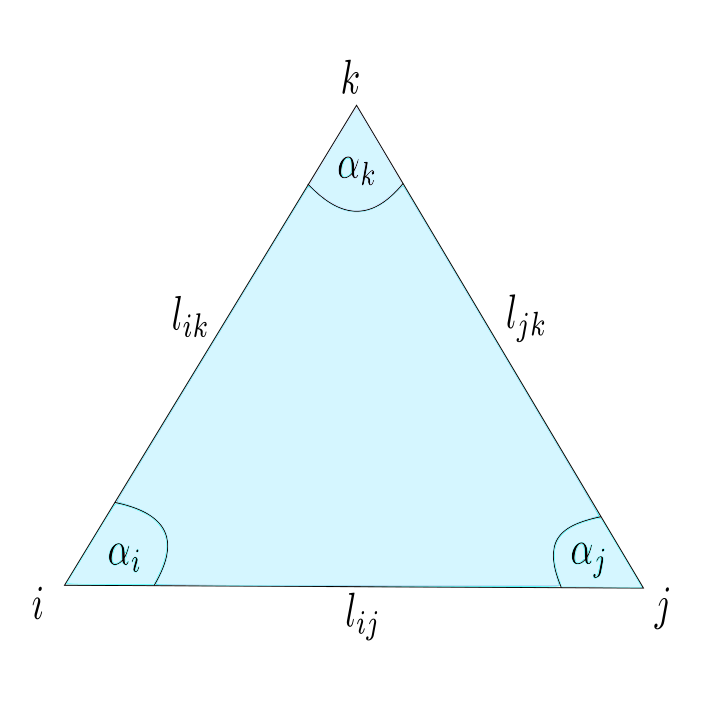Note that every realization $p:V\to {\mathbb{R}}^3$ induces a metric on the underlying triangulated surface. On the other hand a triangulated surface with metric has several realization in ${\mathbb{R}}^3$, such that the metrics coincide. On a triangulated surface with metric every triangle has the structure of an euclidean triangle in ${\mathbb{R}}^2$, that allows us to interpolate $f:V\to \mathbb{R}$ to a piecewise affine function $\tilde{f}:C\left(\mathrm{\Sigma }\right)\to \mathbb{R}$ and define the Dirichlet energy $E_D(f)$ as in the last lectures.

 In particular, we can define angles and area using the cosine theorem:
$$\cos ({\alpha }_i)=\frac{l_{jk}^2-l_{ji}^2-l_{ki}^2}{2l_{ki}{l}_{ij}}$$
By the triangle inequalities we obtain that $0<\gamma <\pi$ and the angles are well defined. With $\sin ({\alpha }_i)=\sqrt{1-\cos ({\alpha }_i{)}^2}$ we can define the cotangents weights and the area of the triangle $\sigma =\{i,j,k\}$ :
$$A_{\sigma }=\frac{1}{2}\sin ({\alpha }_i)l_{ij}{l}_{ki}.$$
For a realization $p$ of $\mathrm{\Sigma }$ with vertex positions $p_i,p_j,p_k$ and edges $e_{ij}=p_j-p_i,\dots$ we obtain for $\sigma =\{i,j,k\}\in F$:
$$A_{\sigma }(p)=\frac{1}{2}|(p_j-p_i)\times (p_k-p_i)|=\frac{1}{2}|e_{ij}\times e_{ik}|=\frac{1}{2}\sin ({\alpha }_i)\underset{=l_{ij}}{\underbrace{|e_{ij}|}}\underset{=l_{ki}}{\underbrace{|e_{ki}|}},$$
and the total area is give by:
$$A(p)=\sum _{\sigma \in F}{A}_{\sigma }(p).$$

Definition: The following problem is the Plateau problem: Let $\mathrm{\Sigma }$ be a triangulated surface with boundary and $q:V^{\partial }\to {\mathbb{R}}^3$ a prescribed function. We are looking for a realization $p:V\to {\mathbb{R}}^3$ of $\mathrm{\Sigma }$ such that:

1.  ${p|}_{V^{\partial }}=q,$
2.  $p$ has the smallest area among all realizations $\tilde{p}$ of $\mathrm{\Sigma }$, with ${\tilde{p}|}_{V^{\partial }}=q$.

In order to be able to solve the  Plateau problem we have to consider variations of $p$:

Definition: A variation of $p$ with constant boundary assigns to each vertex  $i\in V$ a curve $t\mapsto p_i(t),$ $t\in (-ϵ,ϵ),$ such that:

1. $p_i(0)=p_i$ for all $i\in V.$
2. $p_j(t)=q_j$ for all $t\in (-ϵ,ϵ)$ if $j\in V^{\partial }$.

Definition: $p$ is called a minimal surface if it is a critical point of the area functional, i.e. :
$${\frac{\partial }{\partial t}|}_{t=0}A(p(t))=0,$$
for all variations of $p$ with constant boundary.

Lemma: $p$ is a minimal surface if and only if For each $i\in \stackrel{\circ }{V}$ and each curve $t\mapsto p_i(t),$ $t\in (-ϵ,ϵ)$ we have:
$${\frac{\partial }{\partial t}|}_{t=0}A(p_i(t))={\frac{\partial }{\partial t}|}_{t=0}\sum _{\sigma \in F|i\in \sigma }{A}_{\sigma }(p_i(t))=0.$$

I.e. $p$ is a critical point of the area functional with respect to all variations with constant boundary, if and only if it is a critical point for all those variations that only move one interior vertex.

Proof: $”\Rightarrow ”:$ clear.
$”\Leftarrow :”$ Similar to the following fact from analysis:
All directional derivatives of a function $f:U\to \mathbb{R},U\subset {\mathbb{R}}^n$ vanish at $p\in U$ if and only if all partial derivatives of $f$ vanish at $p$.

Theorem: $p$ is a minimal surface if and only if all tree components of $p$ are discrete harmonic functions with respect to the metric induced on $\mathrm{\Sigma }$ by $p$.

Proof: 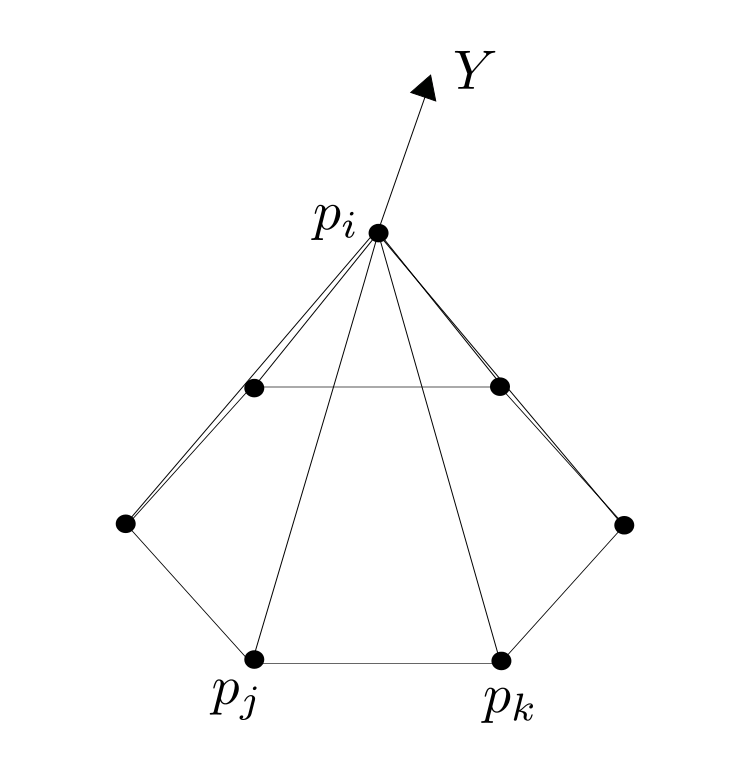Fix $i\in \stackrel{\circ }{V}$ and let  $t\mapsto p_i(t),$ $t\in (-ϵ,ϵ)$ be a variation, that only moves $p_i$ and $Y:=p_i^{\prime }(o).$ Further we define $\hat{F}:=\{\{i,j,k\}\in F|\text{ positive oriented}\}$ to be the set of positive oriented triangles that contain the vertex $i$. We have to show that there holds:
$$\begin{array}{rl}0={\frac{\partial }{\partial t}|}_{t=0}A(p_i(t))& ={\frac{\partial }{\partial t}|}_{t=0}\sum _{\{i,j,k\}\in \hat{F}}|(p_j-p_i(t))\times (p_k-p_i(t))|\\ & ={\frac{\partial }{\partial t}|}_{t=0}\sum _{\{i,j,k\}\in \hat{F}}|e_{ij}(t)\times e_{ik}(t)|.\end{array}$$

Before we start with the proof remember these identities from analysis$\mathrm{\setminus }$linear algebra

1.  For a function $t\to v(t)\in {\mathbb{R}}^3$ there holds:
$$\begin{array}{r}|v{|}^{\prime }=\frac{⟨v,v^{\prime }⟩}{|v|}\end{array}$$
2. For $a,b,c,d\in {\mathbb{R}}^3$ we have:
$$\begin{array}{r}⟨a\times b,c\times d⟩=det\left(\begin{array}{cc}⟨a,c⟩& ⟨a,d⟩\\ ⟨b,c⟩& ⟨b,d⟩\end{array}\right)=⟨a,c⟩⟨b,d⟩-⟨a,d⟩⟨b,c⟩.\end{array}$$
With $e_{i,j}=p_j-p_i$ we get $\dot{e_{ij}}=-Y$ and can compute now the variation of the area functional:
$$\begin{array}{rl}{\frac{\partial }{\partial t}|}_{t=0}& A(p_i(t))=\frac{1}{2}\sum _{\{i,j,k\}\in \hat{F}}\frac{⟨e_{ij}\times e_{ik},-Y\times e_{ik}–e_{ij}\times Y⟩}{|e_{ij}\times e_{jk}|}\\ & =\sum _{\{i,j,k\}\in \hat{F}}\frac{-⟨e_{ij},Y⟩|e_{ik}{|}^2+⟨e_{ik},Y⟩⟨e_{ij},e_{ik}⟩-⟨e_{ik},Y⟩|e_{ij}{|}^2+⟨e_{ij},Y⟩⟨e_{ij},e_{ik}⟩}{2|e_{ij}\times e_{jk}|}\\ & =⟨Y,\sum _{\{i,j,k\}\in \hat{F}}\frac{-e_{ij}|e_{ik}{|}^2-e_{ik}|e_{ij}{|}^2+⟨e_{ij},e_{ik}⟩(e_{ij}+e_{ik})}{2|e_{ij}\times e_{jk}|}⟩\\ & =⟨Y,\sum _{\{i,j,k\}\in \hat{F}}\frac{(-⟨e_{ik},e_{ik}⟩+⟨e_{ij},e_{ik}⟩)e_{ij}+(-⟨e_{ij},e_{ij}⟩+⟨e_{ij},e_{ik}⟩)e_{ik}}{2|e_{ij}\times e_{jk}|}⟩.\end{array}$$
With $$-⟨e_{ik},e_{ik}⟩+⟨e_{ij},e_{ik}⟩=⟨e_{ik},e_{ij}-e_{ik}⟩=⟨e_{ik},e_{kj}⟩,$$
and
$$-⟨e_{ij},e_{ij}⟩+⟨e_{ij},e_{ik}⟩=⟨e_{ij},e_{ik}-e_{ij}⟩=⟨e_{ij},e_{jk}⟩,$$
We have:
$${\frac{\partial }{\partial t}|}_{t=0}A(p_i(t))=⟨Y,\sum _{\{i,j,k\}\in \hat{F}}\left(\frac{⟨e_{ik},e_{kj}⟩e_{ij}}{2|e_{ij}\times e_{jk}|}\right)+\sum _{\{i,j,k\}\in \hat{F}}\left(\frac{⟨e_{ij},e_{jk}⟩e_{ik}}{2|e_{ij}\times e_{jk}|}\right)⟩.$$

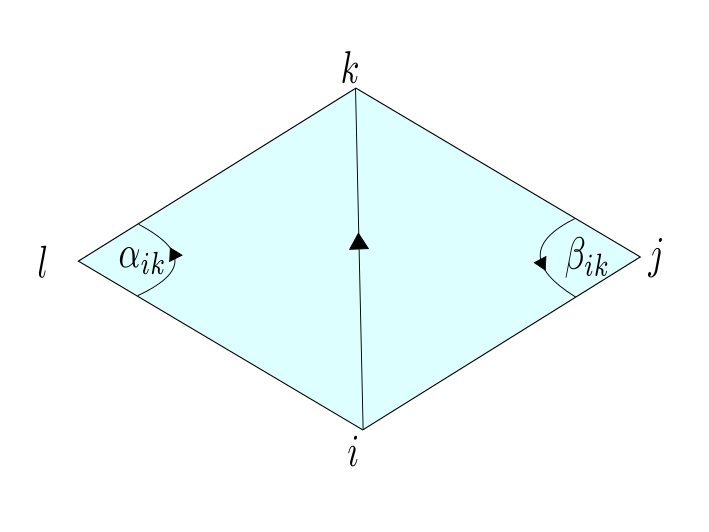
In an earlier lecture  we showed that: $\cot ({\beta }_{ik})=\frac{⟨-e_{ij},e_{jk}⟩}{|e_{ij}\times e_{jk}|}$ and $\cot ({\alpha }_{ik})=\frac{⟨e_{il},e_{kl}⟩}{|e_{ik}\times e_{il}|}.$

With an index shift in the first sum $(i,j,k)\to (i,k,l)$ we have now : $$\begin{array}{rl}{\frac{\partial }{\partial t}|}_{t=0}A(p_i(t))& =⟨Y,-\sum _{\{i,j,k\}\in \hat{F}}\frac{1}{2}(\cot ({\beta }_{ik})+\cot ({\alpha }_{ik}))e_{ik}⟩\\ & =⟨Y,-\sum _{\{i,k\}\in \hat{E}}\frac{1}{2}(\cot ({\beta }_{ik})+\cot ({\alpha }_{ik}))(p_k–p_i)⟩.\end{array}$$

Since this has to hold for all variations $Y$ of $p_i$ and for all $i\in \stackrel{\circ }{V}$we finally get:
$${\frac{\partial }{\partial t}|}_{t=0}A(p(t))=0\iff \sum _{\{i,k\}\in \hat{E}}\frac{1}{2}(\cot ({\beta }_{ik})+\cot ({\alpha }_{ik}))(p_k–p_i)=0\mathrm{\forall }i\in \stackrel{\circ }{V}.$$

This means $p$ is an minimal surface if and only if all components of $p$ are harmonic with respect to the metric on $\mathrm{\Sigma }$ induced by $p$.