Projective transformations
Let $V$, $W$ be two vectorspaces over the same field and of the same dimension and $F\colon V \rightarrow W$ a linear isomorphism. In particular $ker(F) = \{0\}$, so F maps 1-dimensional subspaces to 1-dimensional subspaces.
Hence $F$ induces a map from $P(V)$ to $P(W)$.
Definition: A projective transformation $f$ from $P(V)$ to $P(W)$ is a map defined by a linear isomorphism $F\colon V \rightarrow W$ such that
\begin{equation*}
f([v]) = [F(v)] \quad \forall [v] \in P(V)\,.
\end{equation*}
Proposition. Two linear isomorphisms $F, \tilde{F}: V \rightarrow W$ induce the same projective transformation if and only if $F = \lambda\tilde{F}$ for some $\lambda \neq 0$.
Proof. “$\Leftarrow$”: If $F=\lambda\tilde{F}$ then
\begin{equation*}
f([v]) := [F(v)] = [\lambda\tilde{F}(v)] =
[\tilde{F}(v)] =: \tilde{f}([v]) \hspace{1cm} \forall [v] \in P(V)\,.
\end{equation*}
“$\Rightarrow$”: Let $f: P(V) \rightarrow P(W)$ with $f([v]) = [F(v)] = [\tilde{F}(v)]$.
Hence for every $[v] \in P(V)$ there exists $\lambda_{v} \neq 0$ such that $F(v) = \lambda_{v}\tilde{F}(v)$.
To show: $\lambda_{v} = \lambda$ for some $\lambda \neq 0$ and all $[v] \in P(V)$.
Let $\{b_1, b_2,\ldots, b_{n+1}\}$ be a basis of $V$. Then there exists $\lambda_i \neq 0$ with
\begin{equation*}
F(b_i) = \lambda_i(\tilde{F})(b_i) \quad \forall i = 1, 2, \ldots , n+1\,.
\end{equation*}
For $[\sum\limits_{i=1}^{n+1}{b_i}]$ there exists $\lambda \neq 0$ such that
\begin{align*}
\sum_{i=1}^{n+1}{\lambda_i\tilde{F}(b_i)} = \sum_{i=1}^{n+1}{F(b_i)} &= F(\sum_{i=1}^{n+1}{b_i})=\lambda\tilde{F}(\sum_{i=1}^{n+1}{b_i}) = \sum_{i=1}^{n+1}{\lambda\tilde{F}(b_i)} \\
\Leftrightarrow \sum_{i=1}^{n+1}{(\lambda_i-\lambda)\tilde{F}(b_i)} &= 0\,.
\end{align*}
Since $F$ is a linear isomorphism, $\{F(b_i) \mid i = 1, 2, \ldots , n+1\}$ is a basis of $V$ and in particular linearly independent. Hence $\lambda_i=\lambda$ for all $i = 1, 2, \ldots, n+1$ and $F = \lambda\tilde{F}$.
Definition (projective linear group). The real projective linear group $PGl(n,\mathbb{R})$ is defined as the quotient of the group of linear isomorphisms (the general linear group)
\begin{align*}
\mathrm{GL}(n,\mathbb{R})
&= \{F\colon\R^n \to \R^n \mid \text{F linear isomorphism}\} \\
&= \{A\colon\R^n \rightarrow \R^n \mid n\times n \text{ matrices with } \det(A) \neq 0\}\,.
\end{align*}
by the normal subgroup of non-zero multiples of the identity matrix:
\begin{equation*}
\mathrm{PGL}(n,\mathbb{R}) =
\raise1ex\hbox{$\mathrm{GL}(n,\R)$}\Big/\lower1ex\hbox{$\{\lambda \cdot I_n \mid \lambda \neq 0\}$}\,.\end{equation*}
This is the group of projective transformations from $\RP^{n-1}$ to $\RP^{n-1}$.
Examples.
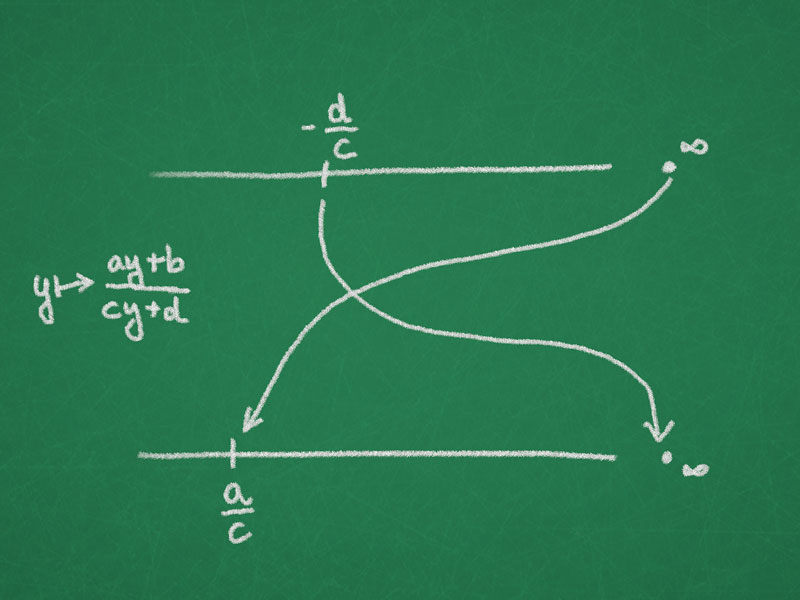
- In terms of affine coordinates projective transformations from $\RP^{1}$ to $\RP^{1}$ are fractional linear transformations.
- Central projections are projective transformations.
Theorem. Let $A_1, A_2, \ldots , A_{n+2}$ and $B_1, B_2, \ldots , B_{n+2}$ be points in general position in the $n$-dimensional projective spaces $P(V)$ und $P(W)$. There exists a unique transformation $f\colon P(V) \to P(W)$ such that $f(A_i)=B_i$.
Proof. Existence: Let $a_i \in V$ such that $A_i=[a_i]$ for all $i=1,\ldots,n+1$ and $A_{n+2}=[\sum\limits_{i=1}^{n+1}{a_i}]$. Analogously, there are $b_i \in V$ such that $B_i=[b_i]$ for all $i=1,\ldots,n+1$ and $B_{n+2}=\left[\sum\limits_{i=1}^{n+1}{b_i}\right]$. Define a linear isomorphism $F\colon V \rightarrow W$ using the bases $\{a_i\}$ and $\{b_i\}$: $F(a_i)=b_i$ for all $i=1,\ldots,n+1$. Then
\begin{equation*}
F(a_{n+2}) = F\left(\sum_{i=1}^{n+1}{a_i}\right) = \sum_{i=1}^{n+1}F(a_i) = \sum_{i=1}^{n+1}{b_i} = b_{n+2}\,.
\end{equation*}
Hence $f([v])=[F(v)]$ is a projective transformation with $f(A_i)=B_i$ $\forall i=1,\ldots,n+2$
Uniqueness: Let $f$ and $\tilde{f}$ be two projective transformations mapping $A_i \to B_i$ and $F$ and $\tilde{F}$ the corresponding linear isomorphisms. Further let $A_i = [a_i]$ and $B_i = [b_i]$ such that $F(a_i) = b_i$ and $a_{n+2} = \sum_{i=1}^{n+1} a_i$ and $b_{n+2} = \sum_{i=1}^{n+1} b_i$. Then for $i = 1,\ldots,n+2$ there exist $\lambda_i \neq 0$ such that $F(a_i) = \lambda_i \tilde{F}(a_i)$. Further
\begin{align*}
\sum_{i=1}^{n+1} \lambda_{n+2} b_i =
\lambda_{n+2} b_{n+2} &=
F(a_{n+2})
\\&= \tilde{F}(a_{n+2}) =
\tilde{F}(\sum_{i=1}^{n+1}a_i) =
\sum_{i=1}^{n+1} \lambda_i b_i.
\end{align*}
This implies that $\lambda_i = \lambda_{n+2}$ for all $i = 1, \ldots, n+1$. So $F = \lambda_{n+2} \tilde{F}$ and $f = \tilde{f}$.