Hyperbolic Geometry
Lorentz Spaces
The vector space $\mathbb{R}^{p+q}$ with the bilinear form
$$ \left<x,y\right>_{p,q} = \sum_{i=1}^{p} x_i y_i – \sum_{i=p+1}^{p+q} x_i y_i $$
is the Lorentz-space $\mathbb{R}^{p,q}$. For our purposes the space $\mathbb{R}^{n,1}$ with scalar product (non-degenerate symmetric bilinear form)
$$ \left<x,y\right>_{n,1} = \sum_{i=1}^{n} x_i y_i – x_{n+1} y_{n+1} $$
is the most important case.
Reminder The orthogonal transformations are denoted by $$ O(p,q) = \{f \in GL(p+q,\mathbb{R}) \;|\; \left<f(v),f(w)\right>_{p,q} = \left<v,w\right> \;\forall v,w \in \mathbb{R}^{p+q}\}. $$
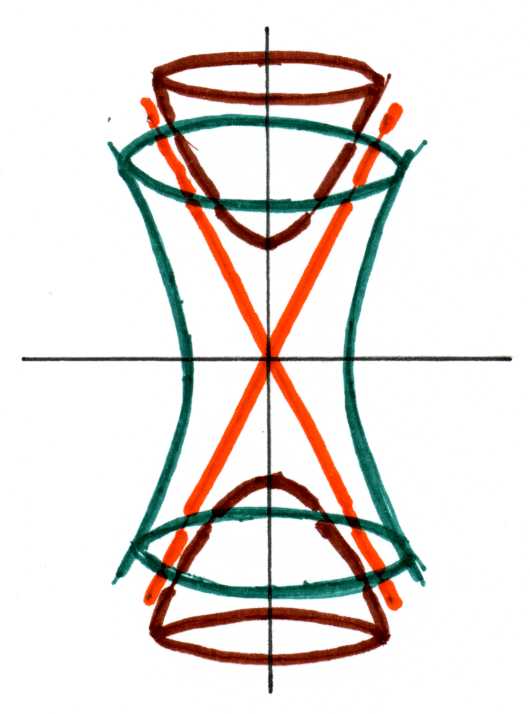
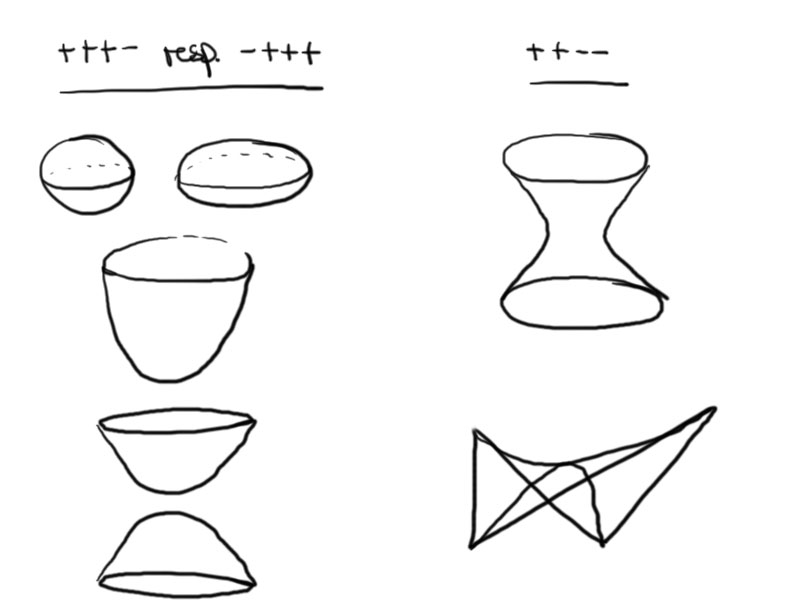
Example $\mathbb{R}^{2,1} \leadsto \mathbb{R}^3$ with $\left<x,y\right>_{2,1} = x_1y_1 + x_2y_2 – x_3y_3$
| • $\left<x,x\right>_{2,1} = x_1^2 + x_2^2 – x_3^2 = -1$ |
time-like vectors $\left<x,x\right>_{2,1} < 0$ |
| • $\left<x,x\right>_{2,1} = 0$ |
light-like vectors $\left<x,x\right>_{2,1} = 0$ |
| • $\left<x,x\right>_{2,1} = 1$ |
space-like vectors $\left<x,x\right>_{2,1} > 0$ |
Hyperbolic Spaces
Definition The $n$-dimensional hyperbolic space is
$$ H^n = \{ x\in \mathbb{R}^{n,1} \;|\; \left<x,x\right>_{n,1} = \sum_{i=1}^{n} x_i^2 – x_{n+1}^2 = -1,\; x_{n+1} > 0 \}. $$
The length of a curve $\gamma : [a,b] \rightarrow H^n$ is defined by
$$ \mathrm{length}(\gamma) = \int_a^b \sqrt{\left<\gamma'(t),\gamma'(t)\right>_{n,1}}\:dt.$$
Why is $\left<\gamma'(t),\gamma'(t)\right>_{n,1} > 0$?
The tangent space at a point $p \in H^n$ is the orthogonal complement $p^\perp$ of $p$, $\gamma : [a,b] \rightarrow H^n$ with $\gamma(t_0) = p$.
\begin{align*}\gamma \in H^n &\Longrightarrow \left<\gamma(t),\gamma(t)\right>_{n,1} = -1 \\&\Longrightarrow 2\left<\gamma(t),\gamma'(t)\right>_{n,1} = 0.\end{align*}
The scalar product of $p$ is $\left<p,p\right>_{n,1} = -1$. Construct a basis $\{p,b_1,\ldots,b_n\}$ with $\left<p,b_i\right>_{n,1} = 0$. Then the matrix of $\left<\cdot,\cdot\right>_{n,1}$ has the form
$$\left( \begin{array}{rc} -1 & 0 \\ 0 & \left( \begin{array}{cc} & \\ & \end{array} \right) \end{array} \right) \Longrightarrow \mathrm{signature}(\left<\cdot,\cdot\right>_{n,1}|_{p^\perp})\text{ is }(n,0).$$
$\leadsto$ On the tangent spaces of the hyperbolic space embedded in $\mathbb{R}^{n,1}$ we obtain a positive-definite scalar product by restricting $\left<\cdot,\cdot\right>_{n,1}$.
$\longrightarrow$ Riemannian manifolds.
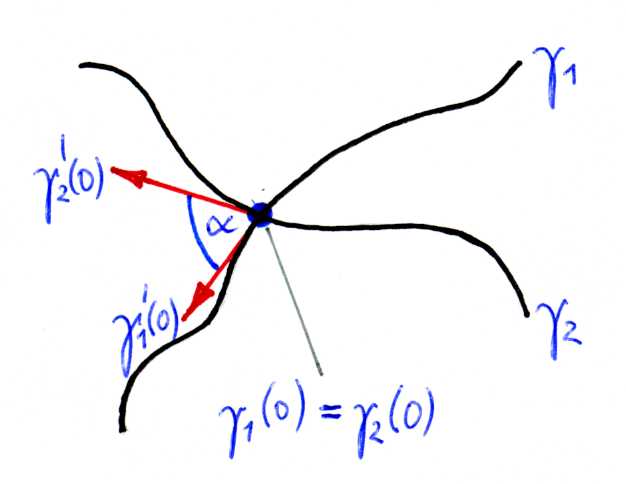
We can measure angles between curves:
$$ \cos\alpha = \frac{\left<\gamma’_1(0), \gamma’_2(0)\right>_{n,1}} {\sqrt{\left<\gamma’_1(0), \gamma’_1(0)\right>_{n,1} \left<\gamma’_2(0), \gamma’_2(0)\right>_{n,1}}} $$
for $\gamma_1,\gamma_2$ in hyperbolic space.
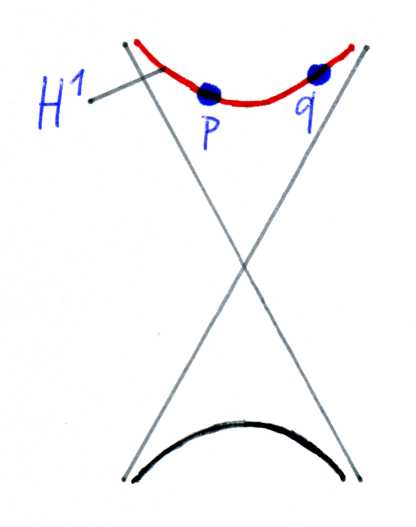
The Hyperbolic Line
The hyperbolic line $H^1 \subset \mathbb{R}^{1,1}$ is given by $\{x\in \mathbb{R}^{1,1} \;|\; x_1^2 – x_2^2 = -1,\; x_2>0\}$. We want to measure the length of the curve $\gamma$ in $H^1$ connecting two points $p,q$.
A parametrization of $H^1 \subset \mathbb{R}^{1,1}$ is given by $\gamma : \mathbb{R} \longrightarrow H^1,\quad t \longmapsto {\sinh t \choose \cosh t}$. Then
$$\left<\gamma(t), \gamma(t)\right>_{1,1} = \sinh^2t – \cosh^2t = -1.$$
Let $p = \gamma(s_1)$ and $q = \gamma(s_2)$ where $s_1 < s_2$. Then, since $\gamma'(t) = {\cosh t \choose \sinh t}$,
\begin{align*}
\mathrm d(p,q) &= \mathrm{length}(\gamma|_{[s_1,s_2]}) = \int_{s_1}^{s_2} \sqrt{\left<\gamma'(t),\gamma'(t)\right>_{1,1}}\:dt = \int_{s_1}^{s_2} \underbrace{\sqrt{\cosh^2t – \sinh^2t}}_{=1}\:dt \\ &= s_2 – s_1.
\end{align*}
$\leadsto$ arc-length parametrization of $H^1$.
For $p$ and $q$ we have
\begin{align*}
\left<p,q\right>_{1,1} &= \left<\gamma(s_1), \gamma(s_2)\right>_{1,1} \\
&= \sinh s_1\sinh s_2 – \cosh s_1\cosh s_2 \\
&= -\cosh(s_2 – s_1) \\ \\
\Longrightarrow \cosh(\mathrm d(p,q)) &= – \left<p,q\right>_{1,1} \\
\mathrm d(p,q) &= \mathrm{arcosh}(-\left<p,q\right>_{1,1}).
\end{align*}
Hyperbolic lines in $H^n$
Definition A hyperbolic line in $H^n$ is the non-empty intersection of $H^n$ with a 2-dim. subspace $U$ of $\mathbb{R}^{n,1}$.
Proposition The restriction of $\left<\cdot,\cdot\right>_{n,1}$ to $U$ has signature $(+-)$.
Proof Since $U \cap H^n\ne\emptyset$ there exists $u\in U$ with $\left<u,u\right> = -1$. Let $\{u,v\}$ be a basis of $U$. Define $$w = v + \left<v,u\right>u = v – \frac{\left<v,u\right>}{\left<u,u\right>}u.$$
Then
\begin{align*}
\left<u,w\right> &= \left<u,v\right> + \left<v,u\right>\underbrace{\left<u,u\right>}_{-1} = 0 \\ \\
\Longrightarrow& w\in u^\perp \\
\Longrightarrow& \left<w,w\right> > 0
\end{align*}
since the signature of $\left<\cdot,\cdot\right>|_{u^\perp}$ is $(++\ldots+)$.
$\Box$
So we can identify $H^n \cap U \subset \mathbb{R}^{n,1}$ naturally with $H^1 \subset \mathbb{R}^{1,1}$.