Fundamental Theorem of real projective geometry: Let $f\colon \RP^n \to \RP^n$, $n \ge 2$, be a bijective map that maps lines to lines. Then $f$ is a projective transformation.
Remark: The theorem does not hold for arbitrary fields. For example $f\colon \CP^n \to \CP^n$ ($n \ge 2$) with
\[f\left(\sqvector{z_1\\ \vdots\\ z_{n+1}}\right) = \sqvector{\bar z_1\\ \vdots\\ \bar z_{n+1}}\]
is a bijective map, mapping complex projective lines to complex projective lines but it is not a projective transformation of $\CP^n$.
Generaliziation for arbitrary fields: A bijective map $f\colon P(V) \to P(V)$, where $V$ is a vectorspace over some field $\mathbb{F}$ that maps lines to lines is induced by an “almost linear” map $F \colon V \to V$, i.e.
\begin{align*}
i)&F(v+w)=F(v)+F(w) &\forall v,w \in V \\
ii)&F(\lambda v) = \alpha (\lambda) F(v) &\forall \lambda \in \mathbb{F}, v\in V, \alpha \colon \mathbb{F} \to \mathbb{F}\,,
\end{align*}
where $\alpha$ is an field automorphism. The only field automorphism of $\R$ is the identity and of $\C$ the complex conjugation.
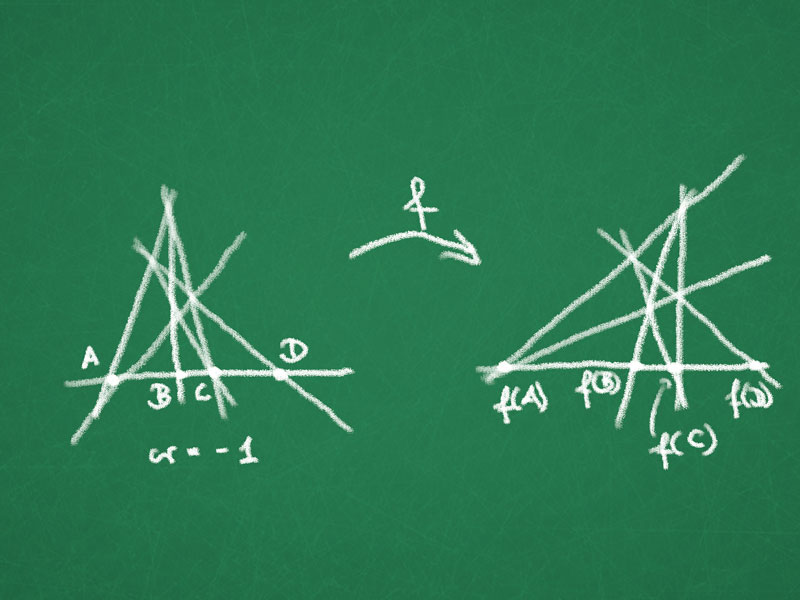
Lemma 1: Let $f\colon \RP^2 \to \RP^2$ be a bijective map that maps lines to lines. Then if $A,B,C,D \in \ell \subseteq \RP^2$ with $\cr(A,B,C,D)=-1$ then $\cr(f(A),f(B),f(C),f(D))=-1$.
Proof: Use theorem on complete quadrilateral.
This implies $\cr(f(A),f(B),f(C),f(D))=-1$.
Lemma 2: Let $f\colon \RP^1 \to \RP^1$ be a bijective map such that $f(0) =0$, $f(1)=1$, $f(\infty)=\infty$ and
$$\cr(A,B,C,D)=-1 \Rightarrow \cr(f(A),f(B),f(C),f(D))=-1\,.$$
Then $f$ is the identity.
Corollary 1: Let $f\colon \RP^1 \to \RP^1$ bijective, such that $\cr(A,B,C,D)=-1$ implies $\cr(f(A),f(B),f(C),f(D))=-1$. Then $f$ is a projective transformation.
Proof: Let $g\colon \RP^1 \to \RP^1$ be a projective transformation such that $g(f(0))= 0$, $g(f(1))= 1$, $g(f(\infty))= \infty$. Then by Lemma 2 we have $g \circ f = id$ and hence $f= g^{-1}$ is a projective transformation.
Proof of Lemma 2: We look at different points on $\RP^1$ that have a cross-ratio of $-1$:
\begin{align*}
i)&\text{cr}(x,\frac{x+y}{2},y ,\infty) = -1\\
&\Rightarrow \text{cr}(f(x),f(\frac{x+y}{2}),f(y) ,\infty) = -1\\
&\Rightarrow -\frac{f(x) – f(\frac{x+y}{2})}{f(\frac{x+y}{2})-f(y)}=-1\\
&\Rightarrow f(\frac{x+y}{2})-f(x) = – f(\frac{x+y}{2})+f(y)\\
&\Rightarrow f(\frac{x+y}{2})=\frac{1}{2} (f(x)+f(y))\\
ii)&\text{cr}(0,x,2x,\infty)=-1 \\
&\Rightarrow \text{cr}(0,f(x),f(2x),\infty)=-1\\
&\Rightarrow \frac{f(x)}{f(x)-f(2x)} = -1 \\
&\Rightarrow f(2x) = 2f(x)\\
iii)&\text{i) and ii)} \\
&\Rightarrow f(x+y) = f(x) + f(y)\\
iv)&0=f(0)=f(x-x)=f(x+(-x))=f(x)+f(-x) \\
&\Rightarrow f(-x)=-f(x)\\
v)&\text{iii) and iv)}\\
&\Rightarrow f(kx) = k f(x) &\forall k \in \mathbb{Z}\\
vi)&v) \Rightarrow f(qx)=qf(x) &\forall q \in \mathbb{Q}\\
& \text{for $x=1$ we obtain } f(q)=q &\forall q \in \mathbb{Q}\\
&\text{We will prove the monotonicity of $f$ on $\mathbb{R}$}\\
vii) &\text{cr}(-x,1,x,x^2) = -1 \\
&\Rightarrow \text{cr}(f(-x),1,f(x),f(x^2))=-1 \\
&\Rightarrow f(x^2)=f(x)^2\\
viii) &x > 0 \Rightarrow f(x)>0& \text{by vii)}\\
ix)&y-x >0 \\
&\Rightarrow f(y-x)>0 \\
&\Rightarrow f(y) -f(x) >0 \\
&\Rightarrow f(y)>f(x)
\end{align*}
Since $f$ is a monotonically increasing function which is the identity on $\mathbb{Q}$, $f$ is the identity.
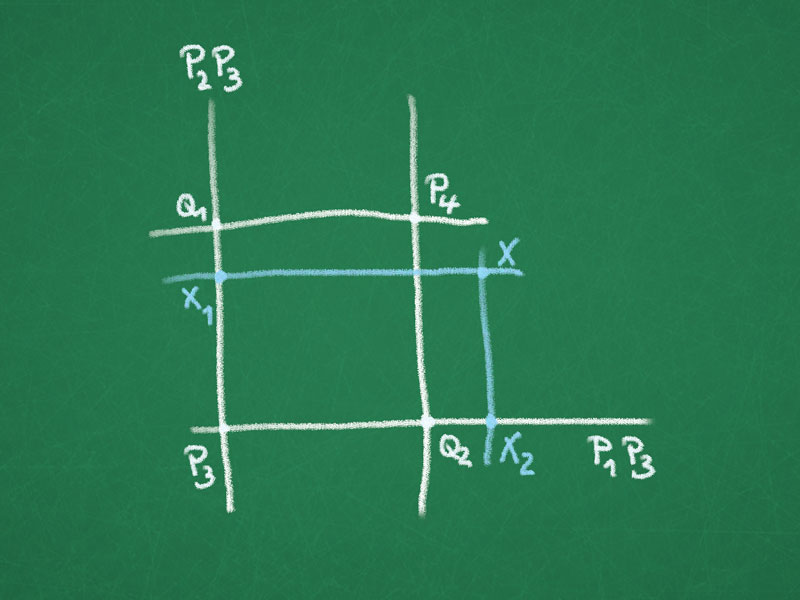
Proof of the fundamental theorem (n=2): Let $f\colon \RP^2 \to \RP^2$ be a bijective map, mapping lines to lines. Let $P_1 = \sqvector{1 \\ 0 \\ 0}$, $P_2 = \sqvector{0 \\ 1 \\ 0}$, $P_3 = \sqvector{0 \\ 0 \\ 1}$, $P_4 = \sqvector{1 \\ 1 \\ 1}$ and $g\colon \RP^2 \to \RP^2$ be a projective transformation such that $g(f(P_i)) =P_i$.
Let $X\in \RP^2$ not on the line $P_1P_2$.
Then the lines $P_iP_j$ are mapped onto themselves since $g \circ f$ fixes the $P_i$ and maps lines to lines. In particular, $g(f(P_2P_3))=P_2P_3$ and $g(f(P_1P_3))=P_1P_3$.
Let $Q_1=P_1P_4 \cap P_2P_3$ and $Q_2=P_2P_4 \cap P_1P_3$.
By Lemma 1 $g \circ f$ preserves cross-ratio of $-1$ and by Corollary 1 the map $g \circ f$ restricted to the lines $P_1P_3$ and $P_2P_3$, resp., is a projective transformation. Since $g \circ f$ has three fixed points on each of the lines $P_1P_3$ and $P_2P_3$ we see that $g \circ f|_{P_1P_3}$ and $g \circ f|_{P_2P_3}$ is the identity.
Let $X_1 = P_1X \cap P_2P_3$ and $X_2=P_2X \cap P_1P_3$ then $X=P_1X_1 \cap P_2X_2$ and $g(f(X_i))=X_i$, $i=1,2$.
So $g(f(X))=X$ since $g(f(P_1X_1))=P_1X_1$ and $g(f(P_2X_2))=P_2X_2$.
Hence $f=g^{-1}$ is a projective transformation (if $X \in P_1P_2$ choose different affine coordinates or note that the point $P_3P_4\cap P_1P_2$ is fixed by $g\circ f$ and $g \circ f$ restricted to the line $P_1P_2$ is again the identity).
Theorem: Let $U \subseteq \RP^n$ be a subset that contains an open ball $B \subset \R^n \subset \RP^n$ (for the decomposition $\RP^n = \R^n \cup \RP^{n-1}$ for some affine coordinate) and $f\colon U \to \RP^n$ an injective map mapping lines to lines, that is, if $\ell$ is a line with $\ell\cap U \neq \emptyset$ then there exists a line $\ell’$ such that $f(U\cap\ell) \subset\ell’$. Then $f$ is the restriction of a projective transformation.
Can you complete the proofs of the following:
1. In Lemma 2: Why is a monotone function on $\R$ that is the identity on $\mathbb{Q}$ the identity?
2. In the proof of the fundamental theorem we assume that that points $f(P_i)$ are in general position. Why is this true? More generally, why are points in general position mapped to points in general position by bijective maps $\RP^n \to \RP^n$ that map lines to lines?
3. How can you generalize the proof of the fundamental theorem to $n > 2$?
Come to the tutorial 🙂