Let $\ell$ be a line in $\RP^2$. Then the line can be described by one homogeneous equation:
$$\begin{bmatrix}
x_1\\
x_2\\
x_3\end{bmatrix}\in l \Longleftrightarrow a_1x_1+a_2x_2+a_3x_3=0\,,$$
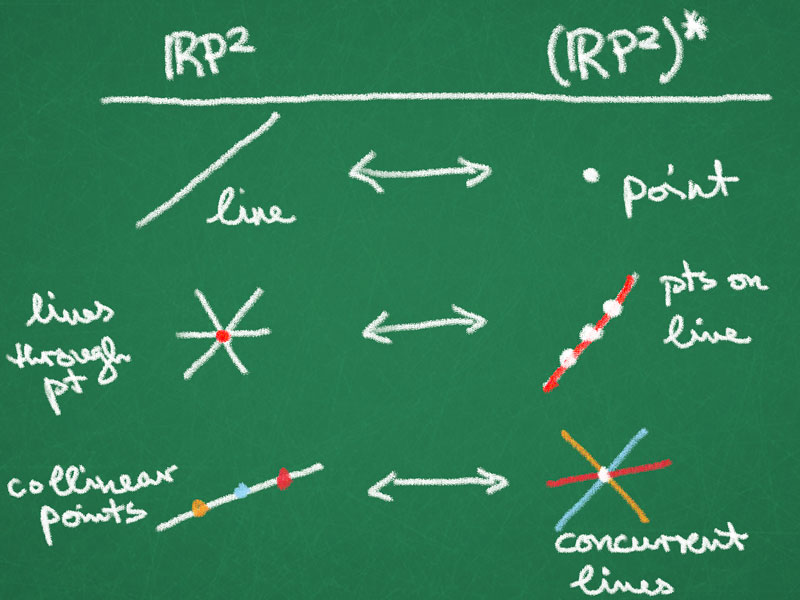
where the $a_i$ are unique up to a scalar multiple $\lambda\neq0$. We can take in a way that will be explained in detail, the point $[a_1,a_2,a_3]^T$ as homogeneous coordinates for the line $\ell$. The lines in $\RP^2$ yield another projective plane with homogeneous coordinates $[a_1,a_2,a_3]^T$. This is what we call the dual projective plane $(\RP^2)^*$. If we fix one point $[x_1,x_2,x_3]^T\in \RP^2$, the set of lines through this point corresponds to a line in $(\RP^2)^*$.
Note: This is the intuition, let’s see the formal definition.
Duality of Vector Spaces
Definition. Let $V$ be a vector space of finite dimension over some field $\mathbb{F}$. The dual vector space is defined as
$$V^*:=\{\phi\colon V\to\mathbb{F} \mid \phi\ \text{is linear}\}\,.$$
Note. If $dim(V)=\infty$, we have to add continuity as a property for the linear function $\phi$.
Let us now consider bases. If $\{b_1,\ldots,b_n\}$ is a basis for $V$, then $\{b_1^*,\ldots,b_n^*\}$ is a basis for $V^*$ (this is called dual basis) where
\[
b_i^*(b_j)=\delta_{ij}.
\]
Is easy to check that is a basis for $V^*$ so $dim(V)=dim(V^*)$.
Remark. To identify $V$ with $(V^*)^*$ we don’t need a basis of $V$. A vector $v\in V$ can be interpreted as a linear functional of $V^*$ as
\[
V\to(V^*)^*\,,\ v\mapsto v(\cdot)
\]
with $v(\phi)=\phi(v)$ for any $\phi\in V^*$. But this construction cannot be made in infinite dimension, and in general $V=(V^*)^*$ does not hold.
Definition. If $f\colon V\to W$ is a linear map, then the dual map $f^*$ is defined as
\[
f^*\colon W^*\to V^*\,,\ \psi\mapsto f^*(\psi)
\]
with $f^*(\psi)(v)=\psi(f(v))$ for $v\in V$.
Definition. Let $U\subset V$ a vector subspace, then the annihilator of $U$ is defined as
$$U^{\circ}:=\{\phi\in V^*\mid \phi(u)=0\ \text{for all}\ u\in U\}$$
and is a subspace of $V^*$.
For the dimensions of $U$ and $U^{\circ}$ we have that
$$dim(U)+dim(U^{\circ})=dim(V)\,.$$
Remark.The following properties hold:
- $(U_1\cap U_2)^{\circ}=U_1^{\circ}+U_2^{\circ}$,
- $(U_1+ U_2)^{\circ}=U_1^{\circ}\cap U_2^{\circ}$.
In an euclidean vector space (a vector space of finite dimension over $\R$ endowed with an inner product) one can identify $V$ and $V^*$ canonically and up to these identification $U^{\circ}=U^{\perp}$.
Projective Duality
Definition. Let $P(V)$ a projective space. Then we define the dual projective space as $P(V^*)$.
Examples.
- A point $[v]\in P(V)$ corresponds to a ayperplane $P(\operatorname{span}(v)^{\circ})\subset P(V^*)$.
- Points $[\psi]\in P(\operatorname{span}(v)^{\circ})$ correspond to hyperplanes through $[v]\in P(V)$.
- More generally, the dual of a $k$-plane in $P(V)$ corresponds to an $(n-k-1)$-plane if $dim P(V)=n$.
- Points in the dual $(n-k-1)$-plane correspond to hyperplanes containing the given $k$-plane.
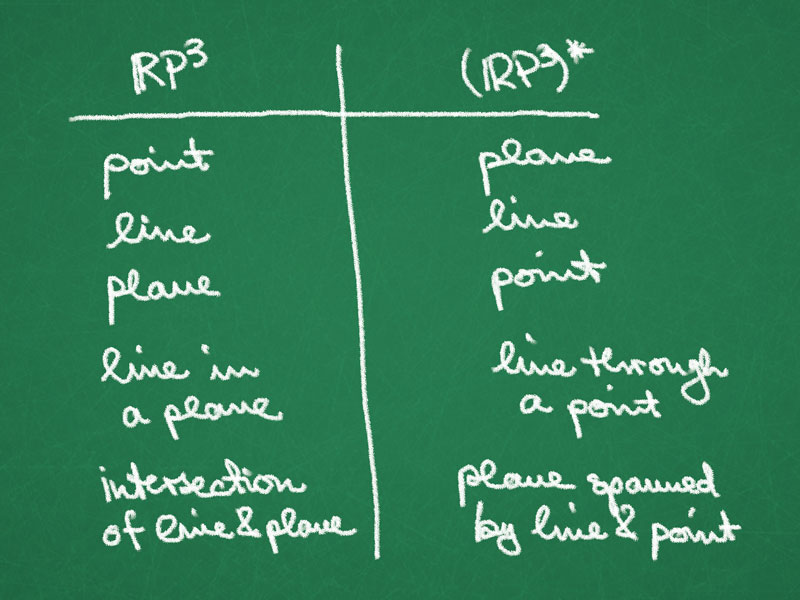
Dictionary for Duality of $\RP^3$
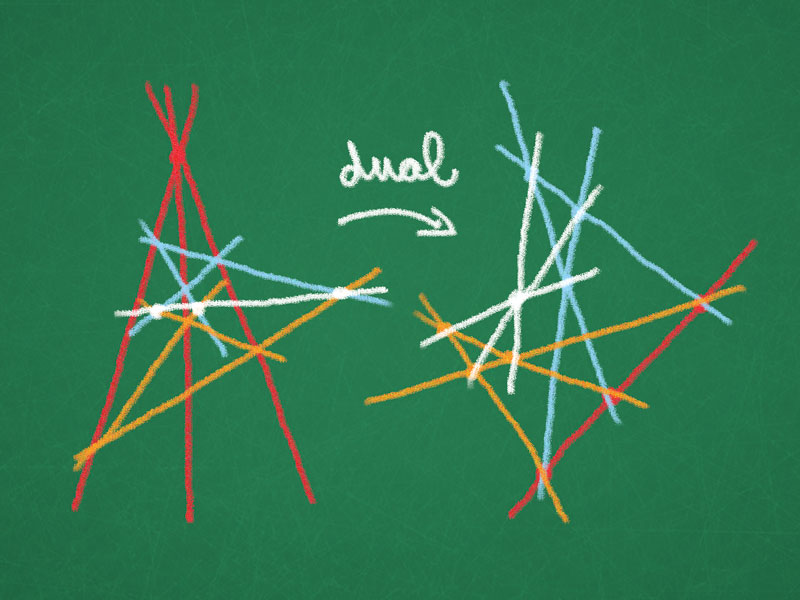
Remark. To every incidence configuration we may associate a dual configuration.
Example. Desargues configuration.