Hyperbolic tilings
In the last lecture we had a look at tilings of the hyperbolic plane. We want to tile the plane with regular $p$-gons, such that at each vertex $q$ polygons meet. Then we do a little calculation and see that for $\frac1p+\frac1q < \frac12$ there exist such tilings of the hyperbolic plane.
These tilings can be generated by a software written by Martin von Gagern from TU Munich. It is written in Java and can be downloaded from his website. I created an Escher like picture with it 🙂
 The original can be found here. And another fun example — just try and enjoy.
The original can be found here. And another fun example — just try and enjoy.
Pencils of circles
A circle in the plane $\R^2 \cup \{\infty\}$ correspond to a space like point in $P(\R^{3,1})$ in the projective model of Möbius geometry.
Definition. A pencil of circles corresponds to a projective line $\ell = P(U)$ in $P(\R^{3,1})$. The bilinear form $\langle.,.\rangle_{3,1}$ restricted to the subspace $U$ can have three different signatures. Depending on the signature we have
- an elliptic pencil if the signature is $(++)$,
- a parabolic pencil if the signature is $(+0)$, or
- a hyperbolic pencil if the signature is $(+-)$.
Using polarity with respect to the quadric in $P(\R^{3,1})$ we obtain the line $\ell^\perp$ polar to $\ell$. This line is again a pencil of circles. The points of the polar line correspond to circles that intersect all circles of first pencil orthogonally. By looking at the signature we see that elliptic and hyperbolic pencils are polars of each other, and that the polar pencil to a parabolic pencil is again parabolic.
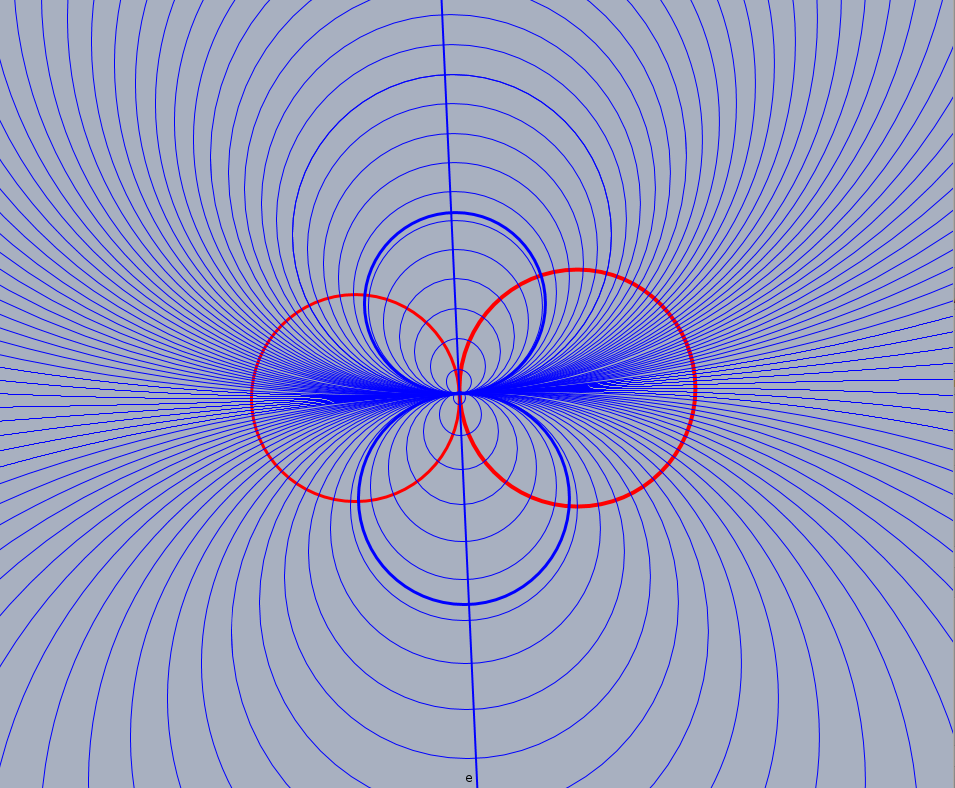
Example. A line in $P(\R^{3,1})$ is generated by two points, i.e., we need two circles to generate a pencil. So let the two red circle generate the pencil and the blue circles belong to the polar pencil.
Two parabolic pencils.
The red circles generate an elliptic pencil and the blue pencil is a hyperbolic pencil.
Now the red circles belong to a hyperbolic pencil and the blue circles form the polar elliptic pencil.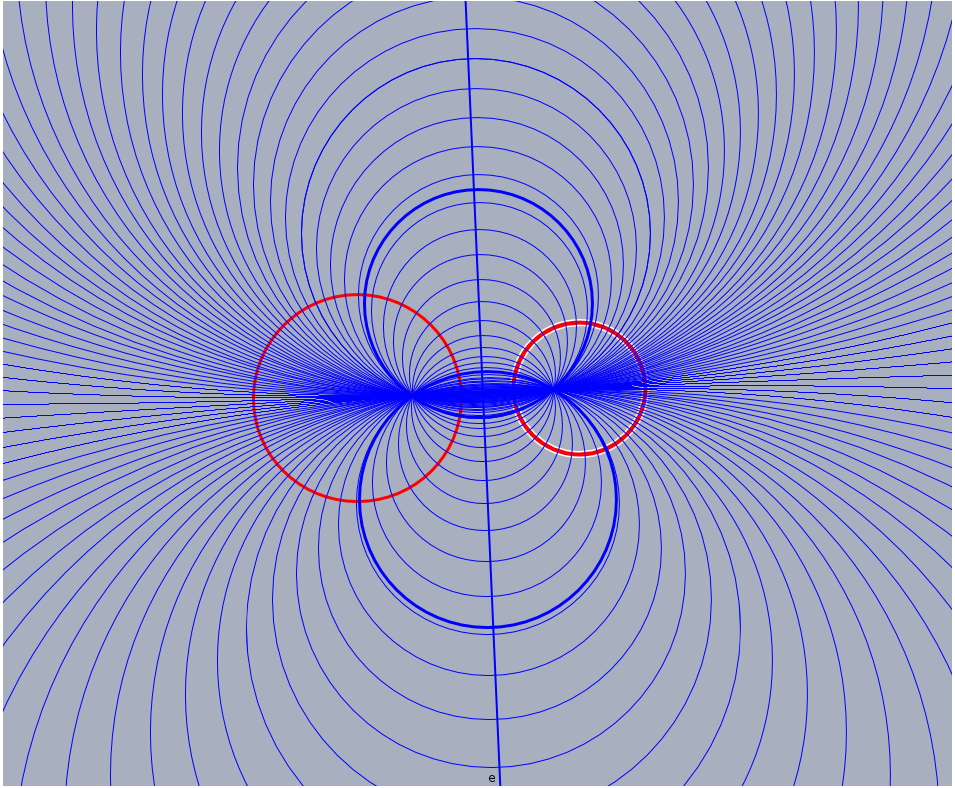
Relation between geometries
We have seen that the group of hyperbolic motions in the projective model of $n$-dimensional hyperbolic space is $PO(n,1)$. The group of Möbius transformation in $n$-dimensional Möbius geometry is $PO(n+1,1)$. So we see a close relation between $(n+1)$-dimensional hyperbolic geometry and $n$-dimensional Möbius geometry. This can be seen best in the respective projective models: $(n+1)$-dimensional hyperbolic geometry deals with the inside of the quadric (the open ball in the Klein model) and $n$-dimensional Möbius geometry deals with the quadric (the $n$-sphere) itself. So Möbius geometry is the geometry of the ideal (infinite) points of hyperbolic $n$-space.
Final remarks
Please have a look at our website for courses of the next semester. I hope you enjoyed the lecture and the experimental blog. Feel free to comment and ask questions to improve the notes.