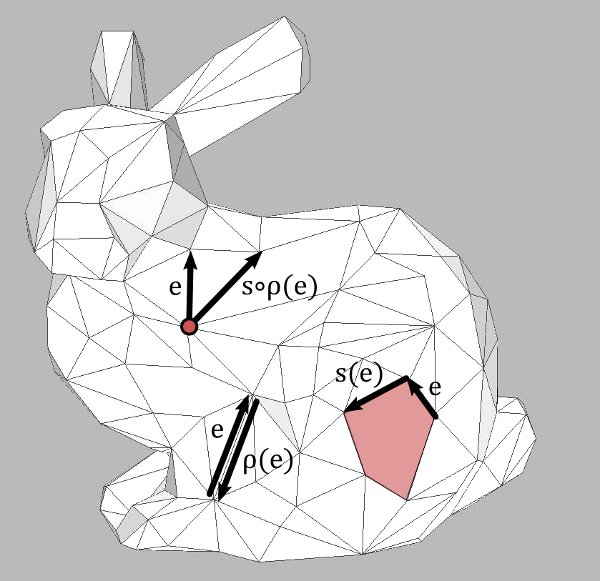
Imagine a cell decomposition $M$ of an oriented compact surface without boundary. Denote by $E$ the set of all oriented edges of $M$. Then for each $e \in E$ there is a unique face $\varphi$ on the left of $e$. Denote by $s(e)$ the oriented edge following $e$ in the cycle of oriented edges in the boundary of $\varphi$. Then
$s: E \rightarrow E$
is a bijective map (a permutation of the elements of $E$). Denote by
$\rho: E \rightarrow E$
the map that assigns to $e$ the same edge with the opposite orientation. Then $\rho$ has no fixed points and satisfies
$\rho^2 = \textrm{id}_E$.
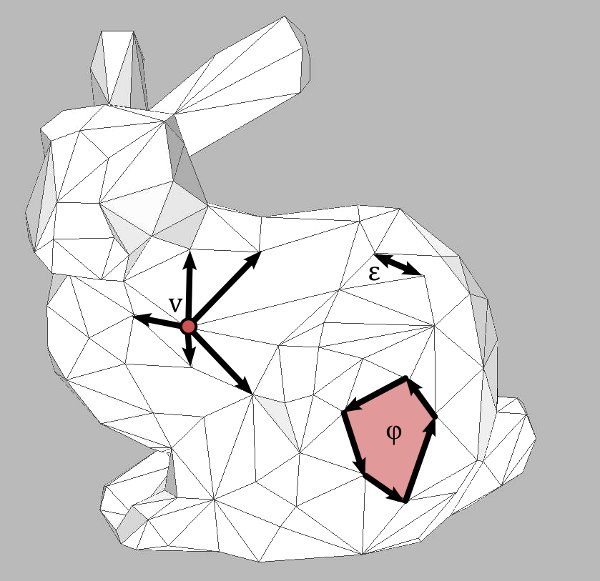
We claim that the whole cell-decomposition can be uniquely recontructed from the permution $s$ and the involution $\rho$ without fixed points: The set of faces $F$ can be recovered from $s,\rho$ as the set of cycles of $s$. A cycle of $s$ is a subset $\varphi \subset E$ which is invariant under $s$ (meaning $s(\varphi) = \varphi$) that cannot be decomposed in any way into smaller invariant subsets. Similarly, the outgoing oriented edges from a vertex $v$ are cycles of the permutation
$s\circ \rho : E \rightarrow E$.
Finally, unoriented edges $\epsilon$ are represented as cycles of $\rho$.