We claim that any pair of permutations $s,\rho$ of a finite set $E$ (with $\rho$ involutive and without fixpoints) defines a unique cell decomposition of some compact surface without boundary. No further conditions are needed. To illustrate this, we look at the simplest possible cases where $E=\{e,\tilde{e}\}$ has only two elements. Then necessarily $\rho(e) = \tilde{e}$ and $\rho(\tilde{e})=e$. For $s$ we have two possibilities:
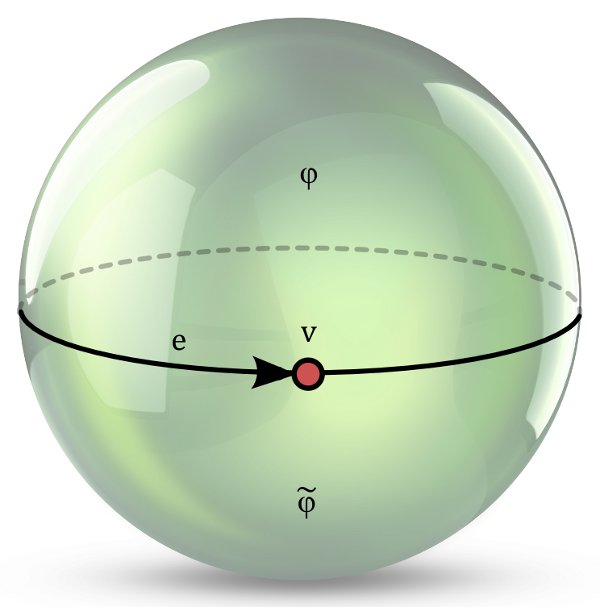
1) $s=id_E$. Then we have two faces, the first one $\varphi$ being bounded by the single edge $e$, the second one $\tilde{\varphi}$ bounded by $\tilde{e}$. We have $s\circ \rho = \rho$ and therefore only one vertex $v$. This is a cell-decomposition of the sphere as shown in the picture below.
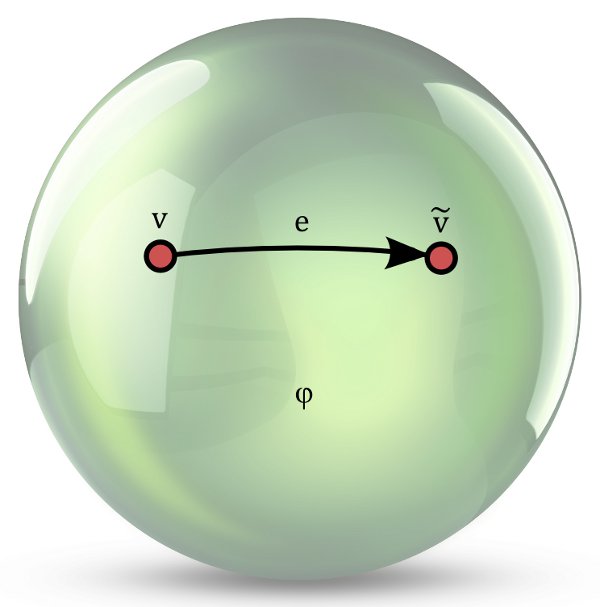
2) $s=\rho$. Then we have only one face bounded by the the edge $e$ followed by the edge $\tilde{e}$. We have $s\circ \rho = id_E$ and therefore two vertices $v$ (with a single outgoing edge $e$) and $\tilde{v}$ (with a single outgoing edge $\tilde{e}$). This is also a cell-decomposition of the sphere.