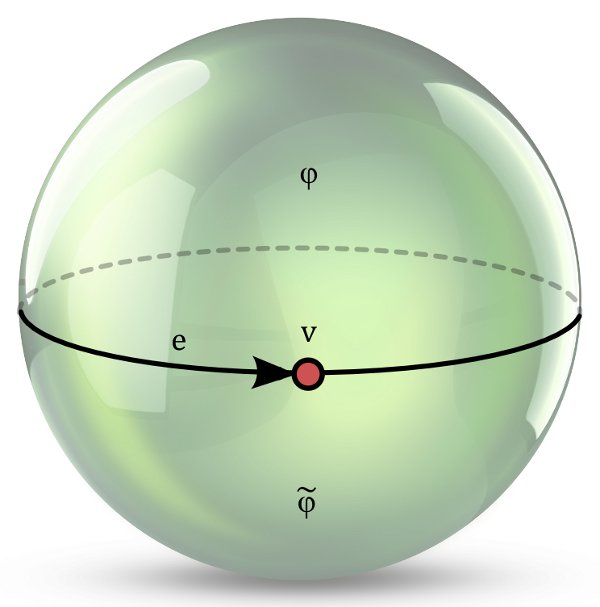
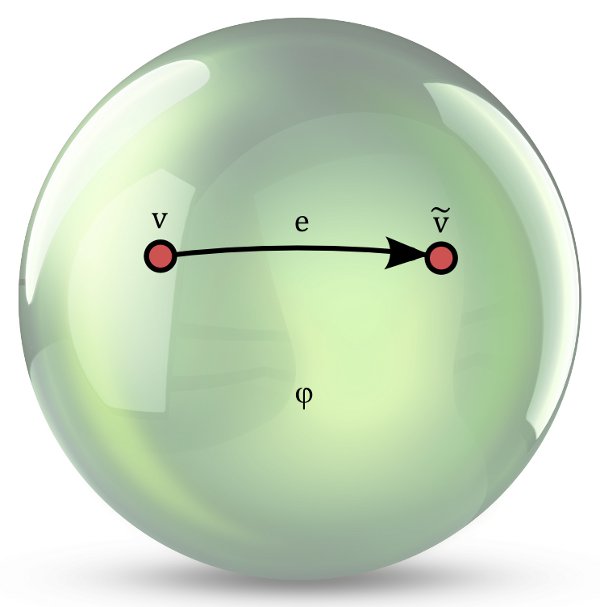
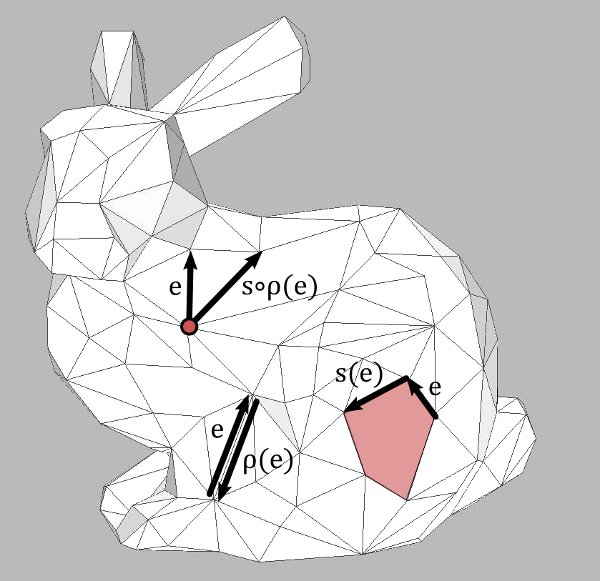
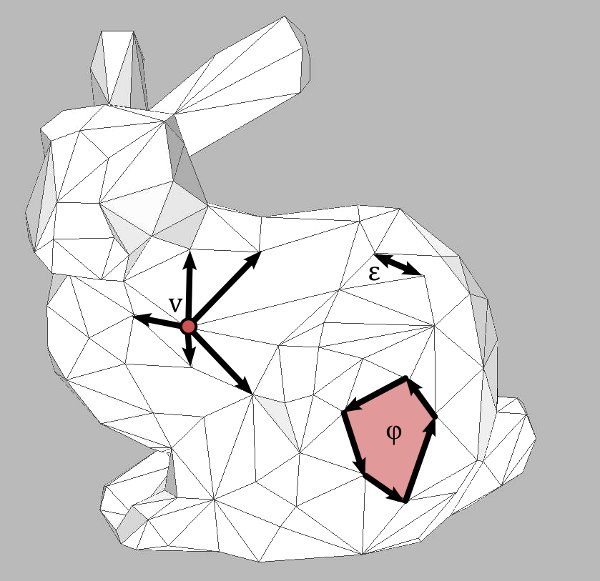
The halfedge description $M=(E,s,\rho )$ of an oriented surface contains all the information. It is nevertheless convenient to introduce some more derived stucture. For an edge $e\in E$ we define

$\text{left}(e)=$ the face (cycle of $s$) containing $e$

$\text{right}(e)=$ the face (cycle of $s$) containing $\rho (e)$

$\text{start}(e)=$ the vertex (cycle of $s\circ \rho$) containing $e$

$\text{end}(e)=$ the vertex (cycle of $s\circ \rho$) containing $\rho (e)$

$\text{unorient}(e)=$ the unoriented edge (cycle of $\rho$) containing $e$.

Denote by $F$ the set of all faces of $M$, by $V$ the set of all vertices and by $\tilde{E}$ the set of all unoriented edges.

If we look at the quintuple $(E,V,\rho ,\text{start},\text{end})$ we see finite sets $E,V$, an involution $\rho :E\to E$ without fixed points and two maps $\text{start},\text{end}:E\to V$ such that

$\text{start}\circ \rho =\text{end}$

This is a one of the possible descriptions of a general finite graph. This graph is called the 1-skeleton or edge-graph of $M$. In a computer graphics context one might also call it the wireframe of $M$.

We claim that any pair of permutations $s,\rho$ of a finite set $E$ (with $\rho$ involutive and without fixpoints) defines a unique cell decomposition of some compact surface without boundary. No further conditions are needed. To illustrate this, we look at the simplest possible cases where $E=\{e,\tilde{e}\}$ has only two elements. Then necessarily $\rho (e)=\tilde{e}$ and $\rho (\tilde{e})=e$. For $s$ we have two possibilities:

1) $s=i{d}_E$. Then we have two faces, the first one $\phi$ being bounded by the single edge $e$, the second one $\tilde{\phi }$ bounded by $\tilde{e}$. We have $s\circ \rho =\rho$ and therefore only one vertex $v$. This is a cell-decomposition of the sphere as shown in the picture below.

2) $s=\rho$. Then we have only one face bounded by the the edge $e$ followed by the edge $\tilde{e}$. We have $s\circ \rho =i{d}_E$ and therefore two vertices $v$ (with a single outgoing edge $e$) and $\tilde{v}$ (with a single outgoing edge $\tilde{e}$). This is also a cell-decomposition of the sphere.

Imagine a cell decomposition $M$ of an oriented compact surface without boundary. Denote by $E$ the set of all oriented edges of $M$. Then for each $e\in E$ there is a unique face $\phi$ on the left of $e$. Denote by $s(e)$ the oriented edge following $e$ in the cycle of oriented edges in the boundary of $\phi$. Then

$s:E\to E$

is a bijective map (a permutation of the elements of $E$). Denote by

$\rho :E\to E$

the map that assigns to $e$ the same edge with the opposite orientation. Then $\rho$ has no fixed points and satisfies

${\rho }^2={\text{id}}_E$.

We claim that the whole cell-decomposition can be uniquely recontructed from the permution $s$ and the involution $\rho$ without fixed points: The set of faces $F$ can be recovered from $s,\rho$ as the set of cycles of $s$. A cycle of $s$ is a subset $\phi \subset E$ which is invariant under $s$ (meaning $s(\phi )=\phi$) that cannot be decomposed in any way into smaller invariant subsets. Similarly, the outgoing oriented edges from a vertex $v$ are cycles of the permutation

$s\circ \rho :E\to E$.

Finally, unoriented edges $ϵ$ are represented as cycles of $\rho$.