Let $M=(E,s,\rho)$ be a discrete surface. The dual surface for $M$ is then the discrete surface
$M^*=(E, s^{-1}\circ \rho, \rho)$.
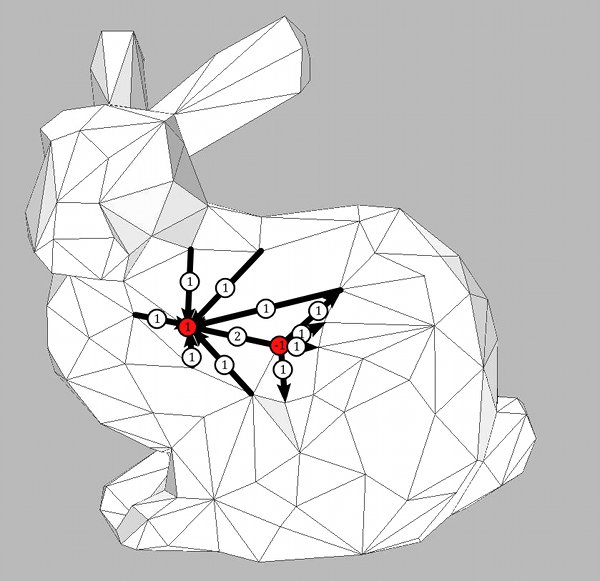
Thus $M^*$ has the same set $E$ of oriented edges as $M$. Also the reversal $\rho$ of edges is the same. The faces of $M^*$ are the cycles of $s^{-1} \circ \rho=\rho \circ(s \circ \rho)^{-1}\circ \rho^{-1}$, which means they are the images under $\rho$ of the vertices of $M$. The vertices of $M^*$ are the cycles of $s^{-1} \circ \rho \circ \rho=s^{-1}$ and therefore are the faces of $M$. To say it briefly: $M^*$ is a surface where the vertices and faces of $M$ have interchanged roles.
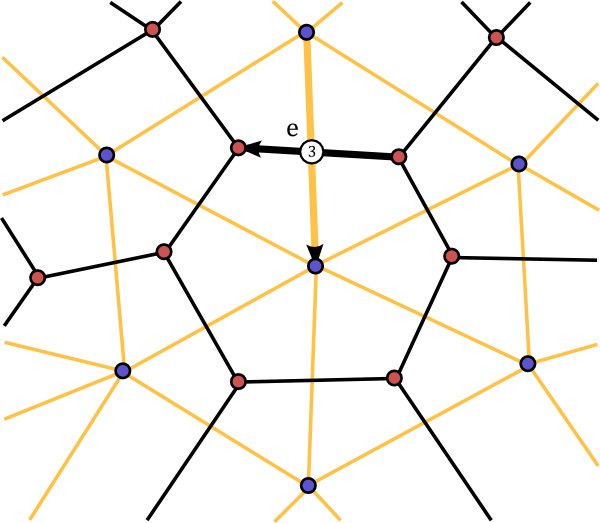
To draw $M^*$ one can draw a new (“dual”) vertex in the middle of every face of $M$ and connect dual vertices whenever the corresponding faces of $M$ are adjacent.
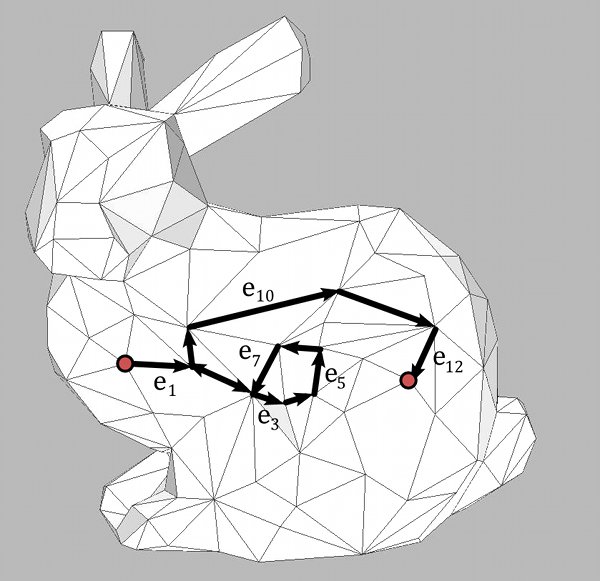
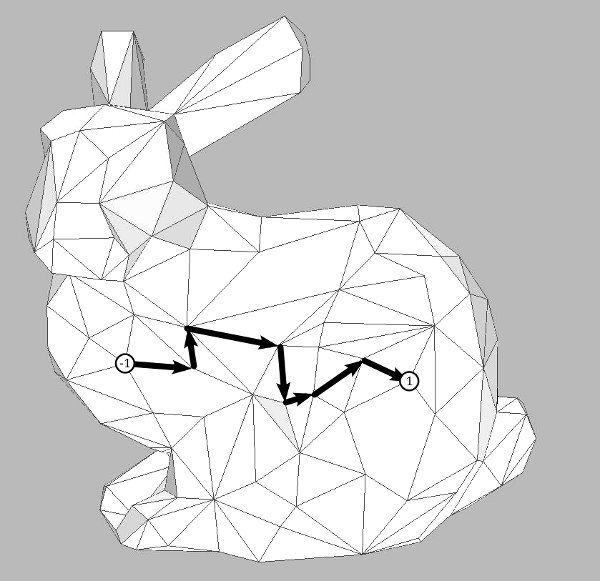
 For every oriented edge $e$ we can draw an arrow from the center of face $\textrm{left}(e)$ to the center of face $\textrm{right}(e)$. So we rotate the arrow representing an oriented edge of $M$ in a clockwise fashion to draw the corresponding edge of $M^*$. We think of this as just another graphical representation for the same oriented edge $e$.
For every oriented edge $e$ we can draw an arrow from the center of face $\textrm{left}(e)$ to the center of face $\textrm{right}(e)$. So we rotate the arrow representing an oriented edge of $M$ in a clockwise fashion to draw the corresponding edge of $M^*$. We think of this as just another graphical representation for the same oriented edge $e$.
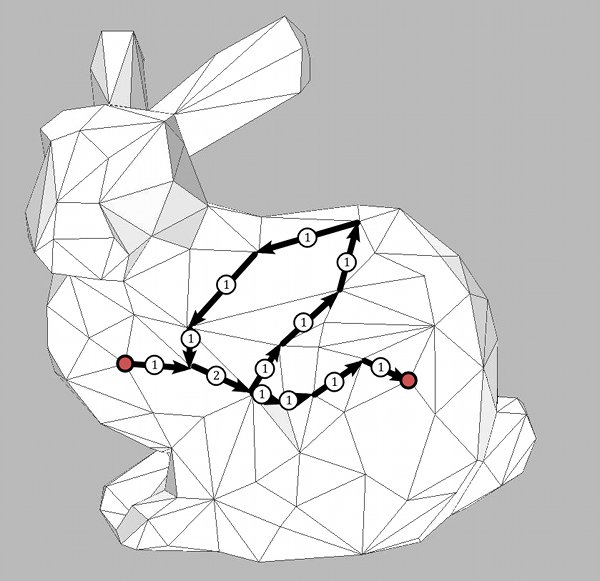
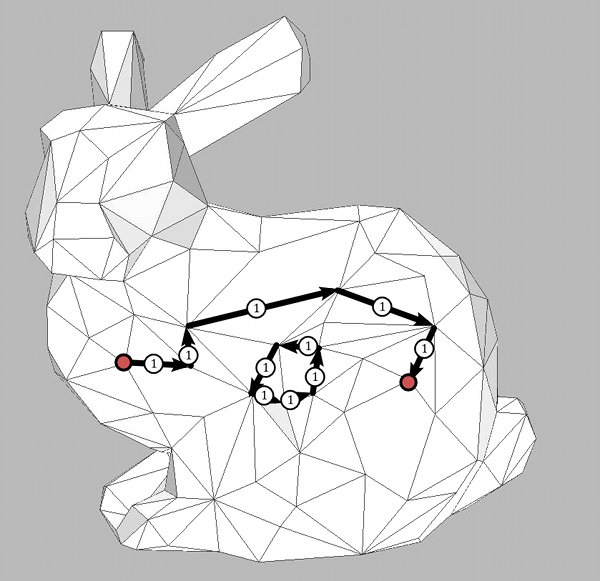
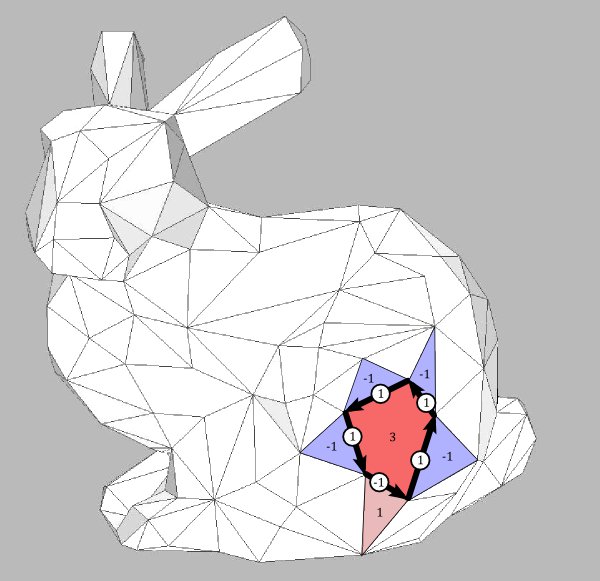
A number written on an oriented edge can mean two different things: First, it could describe the value of a 1-form $\omega$ on $e$. For example, in case $\omega=df$ the number signals the difference of function values of $f$ at the end points. Second, it could describe the value of a dual 1-form $\eta$ on $e$. For example, it could stand for the difference of the values of a dual o-form on the two sides of $e$. It is clear that such a dual 0-form can also be seen as a 0-form on the dual surface $M^*$, justifying our notation $\Omega_0(M^*)$. The same holds for $\Omega_1(M^*)$.