The real projective plane \(\mathbb R\mathrm P^2\) is obtained by identifying the antipodal points of the a \(2\)-sphere \(\mathbb S^2\), i.e. \(\mathbb R\mathrm P^2 = \mathbb S^2/_\sim\) with equivalence relation given by \[ x\sim y \Leftrightarrow y = \pm x.\]
The real projective plane is a sphere with cross-cap – the fundamental polygon looks as follows:

The roman surface: It is known that there exists no embedding of \(\mathbb R\mathrm P^2\) into Euclidean \(3\)-space. Though it can be mapped to \(\mathbb R^3\) with self-intersection. An example is Steiner’s roman surface.
 The corresponding map is given as follows:\[f\colon \mathbb R\mathrm P^2 \to \mathbb R^3, \quad [(x,y,z)]\mapsto \bigl(yz,zx,xy\bigr).\]
The corresponding map is given as follows:\[f\colon \mathbb R\mathrm P^2 \to \mathbb R^3, \quad [(x,y,z)]\mapsto \bigl(yz,zx,xy\bigr).\]
Cross-cap: Actually the roman surface is a projection of the Veronese surface into Euclidean \(3\)-space and as such a special case of a general construction method for non-orientable surfaces. Choosing a different projection we also obtain the cross cap from it:\[f\colon \mathbb R\mathrm P^2 \to \mathbb R^3, \quad [(x,y,z)]\mapsto \bigl(yz,zx,\tfrac{1}{2}(z^2-x^2)\bigr).\]

Boy’s surface: The maps above have singularities and it was not clear that an immersion exists until 1901. At that time Boy discovered an immersion which nowadays is known as Boy’s surface. It can be realized in different ways.
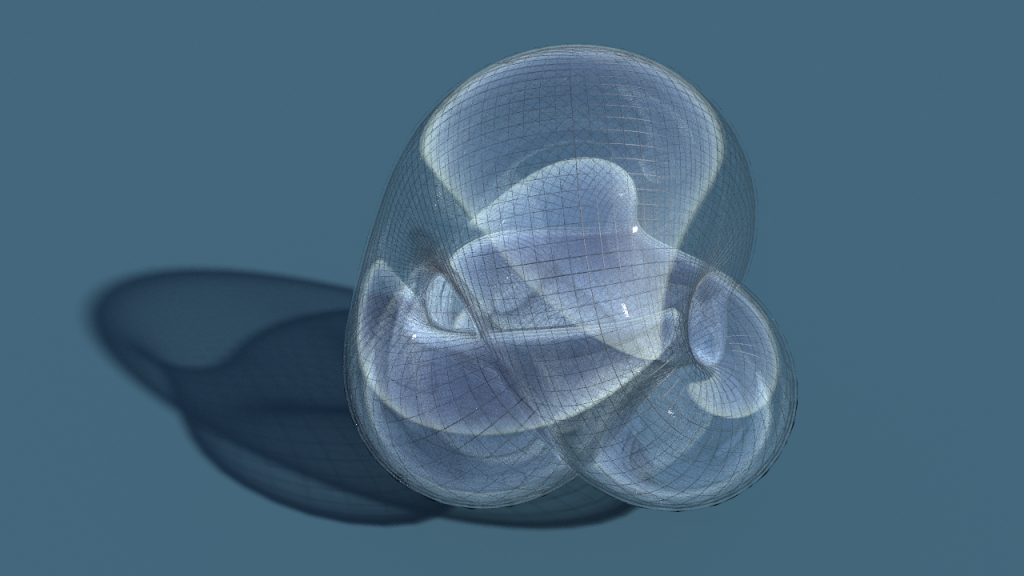 We will use the realization above due to Kusner and Bryant. It is especially beautiful in the sense that it is a critical point of the Willmore energy – a so called Willmore surface.
We will use the realization above due to Kusner and Bryant. It is especially beautiful in the sense that it is a critical point of the Willmore energy – a so called Willmore surface.
It is the inversion of a complete minimal surface with \(3\) ends and as a consequence rational, i.e. the immersion can be written down explicitly with rational functions. Actually it is known that all Willmore surfaces parametrized by spheres are obtained in this way.
This week your task is to visualize Boy’s surface. Its unorientability can be handled similarly to last week’s assignment: Everything will be done on \(\mathbb S^2\)—the orientation cover of \(\mathbb R\mathrm P^2\).
Kusner surfaces: Kusner gave an explicit formula for complete minimal surfaces with ends: Let \(p\in \mathbb N\) and \(r = 2\sqrt{2p-1}/(p-1)\). Let \(z \colon \mathbb S^2 \to \mathbb C\) be the stereographic projection. Then the immersion \(\mathbb S^2 \to \mathbb R^3\) is defined to be the real part of \[\Phi_p = \frac{i}{z^{2p}+rz^p-1}\Bigl(z^{2p-1} – z, -i(z^{2p-1} + z), \tfrac{p-1}{p}(z^{2p} +1)\Bigr).\]
The integer \(p\) controls the symmetry of the immersed surface. Below the surfaces for \(p=3,4,5\) and \(6\). Here we have cut out disks around the poles of \(\mathbb S^2\) for visualization purposes.

Finally we obtain Boy’s surface by a Möbius transformation of the Kusner surface with \(p=3\). The transformation is an inversion in the unit sphere with center \((0,0,h)\), \(h\neq 0\).
Implementation: The implementation is straight forward. The network could look as follows:
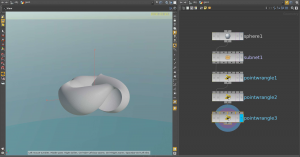 We start with a sphere, apply the stereographic projection (
We start with a sphere, apply the stereographic projection (poinwrangle1), Kusner’s formula (pointwrangle2) and finally the inversion in the sphere (pointwrangle3).
The node subnet1 contains a small network that cuts off a cap from the north pole and a cap from the south pole of the sphere. This can be done by two clip nodes.
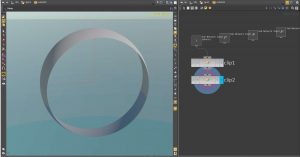 Cutting this holes symmetrically corresponds to cutting a disk from \(\mathbb R\mathrm P^2\). Thus the cylinder above is mapped to a Möbius strip on Boy’s surface.
Cutting this holes symmetrically corresponds to cutting a disk from \(\mathbb R\mathrm P^2\). Thus the cylinder above is mapped to a Möbius strip on Boy’s surface.
 Though the surface is still quite hard to understand from the picture. One way to understand it better is to use a parameter for the width of the strip. Here a sequence for growing width.
Though the surface is still quite hard to understand from the picture. One way to understand it better is to use a parameter for the width of the strip. Here a sequence for growing width.
 If we move the strip up and destroy the symmetry the two sheets of the covering become visible.
If we move the strip up and destroy the symmetry the two sheets of the covering become visible.

Note that a cell decomposition of \(\mathbb R\mathrm P^2\) is basically a cell decomposition of \(\mathbb S^2\) which is mapped by the antipodal map to itself. One way to obtain such a cell decomposition is by subdivision. E.g. we can start with a tetrahedron, then apply on subdivision step using Cutmull–Clark subdivision before we project back to the sphere. To obtain finer meshes one can iterate this.
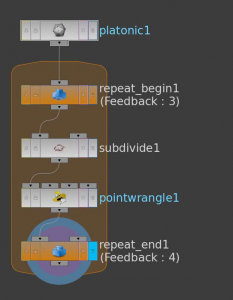 Below a quite coarse parametrization of Boy’s surface.
Below a quite coarse parametrization of Boy’s surface.

Homework (due 14 May): Wire up a network to visualize Boy’s surface. In detail this means:
1) Write a subnet that produces a cell decomposition of \(\mathbb R\mathrm P^2\).
2) Write a subnet that removes disks around north and south pole to obtain a strip.
3) Implement Kusner’s formula and postcompose with the sphere inversion to obtain Boy’s surface.
Build in parameters to control the resolution of the cell-decomposition, the integer \(p\) and the width of the strip.
