While (for good reasons) we have restricted our treatment of combinatorial cell complexes to the two-dimensional case, the theory of $n$-dimensional simplicial complexes is rather straightforward:
Definition: A simplicial complex is a finite set $P$ together with a set $\mathcal{S}$ of subsets $S\subset P$ with the following properties:
(i) For every $i\in P$ we have $\{i\}\in \mathcal{S}$.
(ii) If $S\in\mathcal{S}$ and $T\subset S,\,T\neq \emptyset$ then $T\in \mathcal{S}$.
An element $S\in\mathcal{S}$ is called a simplex of $\mathcal{S}$ of dimension $k$ if the number of its elements equals $k+1$. The set of all $k$-dimensional simplices in $\mathcal{S}$ is called the $k$-skeleton $\mathcal{S}^k$ of $\mathcal{S}$.
A one-dimensional simplicial complex is the same thing as a graph. The one-dimensional simplices of any simplicial complex are called edges, the two-dimensional simplices are called triangles and the three-dimensional ones are called tetrahedra. The picture below shows a graph with $P=\{1,2,3,4,5,6\}$ and seven edges.
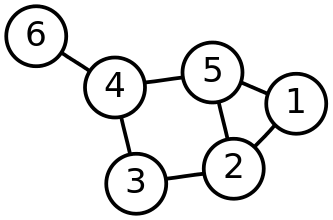
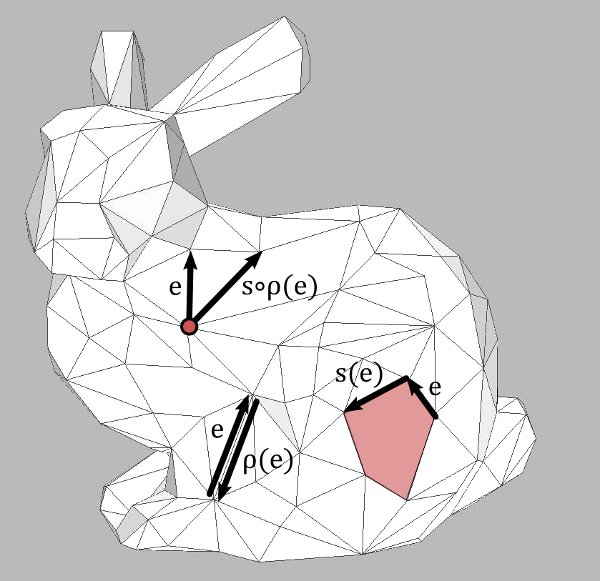
A one-dimensional simplicial complex $\mathcal{S}$ (a graph) can be viewed as a special one-dimensional cell complex $M$ (i.e. a special multigraph). The oriented edges of $M$ is the set of ordered pairs $(i,j)$ with $\{i,j\}\in \mathcal{S}^1$ and the maps $s,d,\rho$ are defined by
\begin{align*}s((i,j))&:=i\\ d((i,j))&:=j \\ \rho((i,j))&:=(j,i).\end{align*}
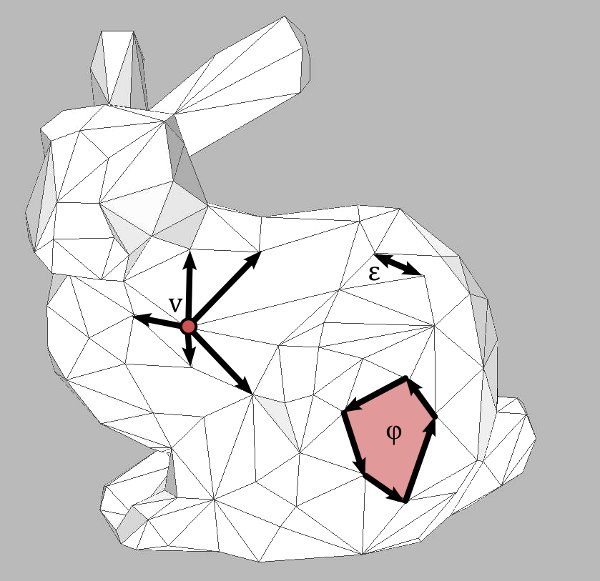
Similarly, a two-dimensional simplicial complex can be viewed as a special two-dimensional cell complex. The cell-complex below from the last post arises in this way from a two-dimensional simplicial complex with five points, ten edges and six triangles.

We have not really discussed this, but a two-dimensional cell complex describes a unique topological space. The same holds for general simplicial complexes. However, simplicial complexes are much more powerful for the discrete modeling of physical objects for the following reason: The topological space described by a combinatorial simplicial complex comes with a canonical piecewise affine structure. We now elaborate what this means.
Let $\mathcal{S}$ be a simplicial complex with point set $P$. Define then the piecewise affine space $C(\mathcal{S})$ corresponding to $\mathcal{S}$ as the set of all functions $f:P\to \mathbb{R}$ such that $f(i)\geq 0$ for all $i\in P$,
$$\sum_{i\in P}\, f(i)=1$$
and
$$\big\{ \,i\in P \,\,\,\big|\,\,\, f(i)\neq 0\,\big\} \in \mathcal{S}.$$
For each simplex $S\in \mathcal{S}$ we define an affine space
$$\mathcal{A}_S:= \bigg\{\, g: P\to \mathbb{R} \,\,\,\bigg|\,\,\,\sum_{i\in P} g(i)=1\mbox{ and }i\notin S \implies g(i)=0 \,\bigg\}$$
The vector space corresponding to the affine space $\mathcal{A}_S$ is
$$V_S:= \bigg\{\, g: P\to \mathbb{R} \,\,\,\bigg|\,\,\,\sum_{p\in P} g(i)=0\mbox{ and }i\notin S \implies g(i)=0 \,\bigg\}$$
and each $\mathcal{A}_S$ is spanned by the simplex
$$\Sigma_S:=\big\{\, g\in\mathcal{A}_{S} \,\,\,\big|\,\,\,g(i)\geq 0 \mbox{ for all } i\in P \,\big\}.$$
The whole space $C(\mathcal{S})$ is the disjoined union of all the interiors (within $\mathcal{A}_S$) of the simplices $\Sigma_S$ for $S\in \mathcal{S}$. If $S\in \mathcal{S}$ and $T\subset S$ then $\mathcal{A}_T$ is an affine subspace of $\mathcal{A}_S$. Similarly, we also have $\Sigma_T \subset \Sigma_S$ in this case.
Each point $i\in P$ corresponds to a particular element $\delta_i\in C(\mathcal{S})$ defined by $\delta_i(j)=1$ for $j=i$ and $\delta_i(j)=0$ otherwise. We have $\mathcal{A}_{\{p\}}=\Sigma_{\{i\}}=\{\delta_i\}$. The main property that makes simplicial complexes useful for physical modeling is the following easy-to-prove
Theorem: Let $\mathcal{S}$ be a simplicial complex with point set $P$ and let $f: P \to V$ be a map into any vector space $V$. Then there is a unique map
$$\hat{f}:C(\mathcal{S})\to V$$
whose restriction to each simplex $\Sigma_S$ is affine and which extends $f$ in the sense that for all $i\in P$ we have
$$\hat{f}(\delta_i)=f(i).$$
In particular, if we have a two-dimensional simplicial complex and are given a position in $\mathbb{R}^3$ for each of its points, it is clear how to fill in the triangles, for example in order to render them.




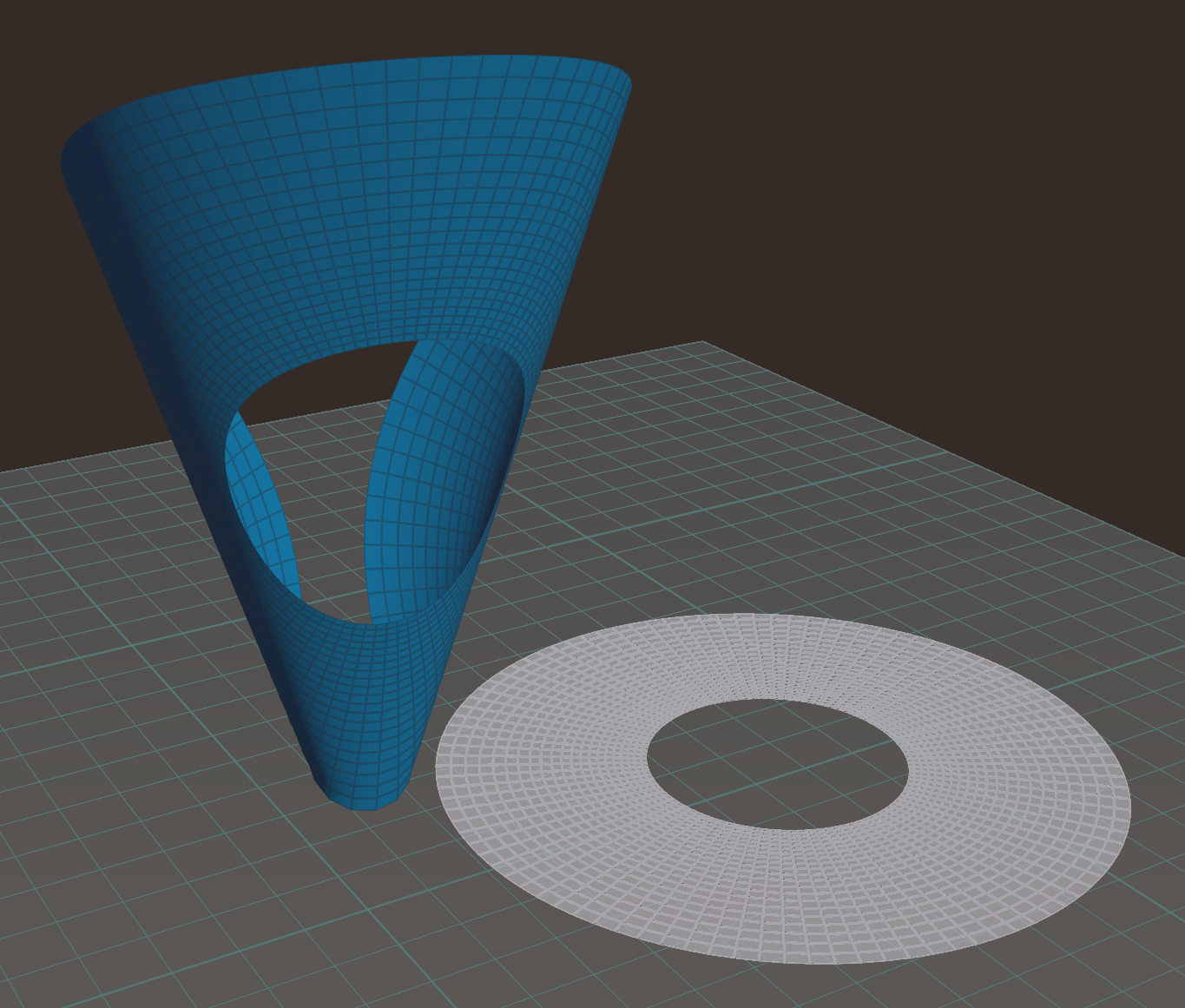

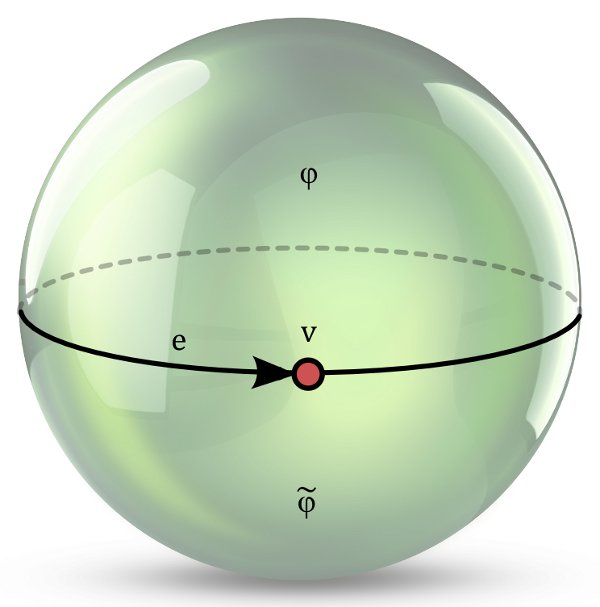
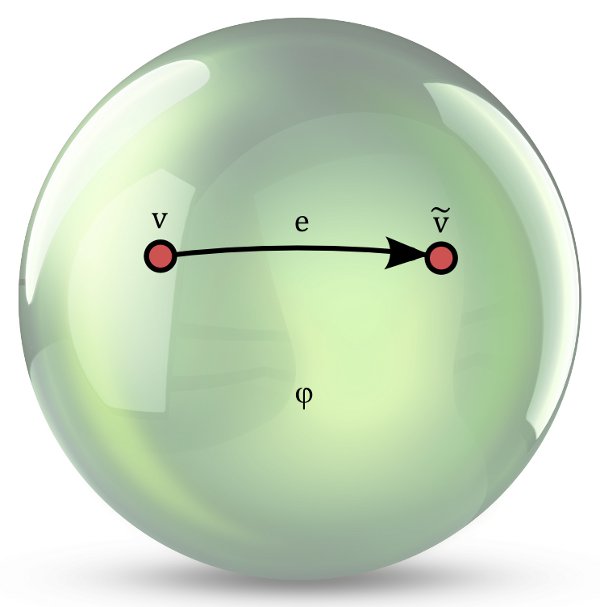
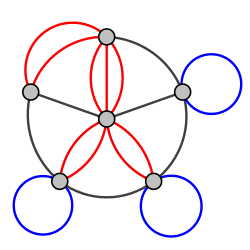
 Note that different faces can have the same edge cycle. This is for example the case for the sphere below, which is represented as a two-dimensional cell complex with six points, six edges and two faces:
Note that different faces can have the same edge cycle. This is for example the case for the sphere below, which is represented as a two-dimensional cell complex with six points, six edges and two faces:
