Proposition
We can identify the Poincaré and the Klein model by the following construction:
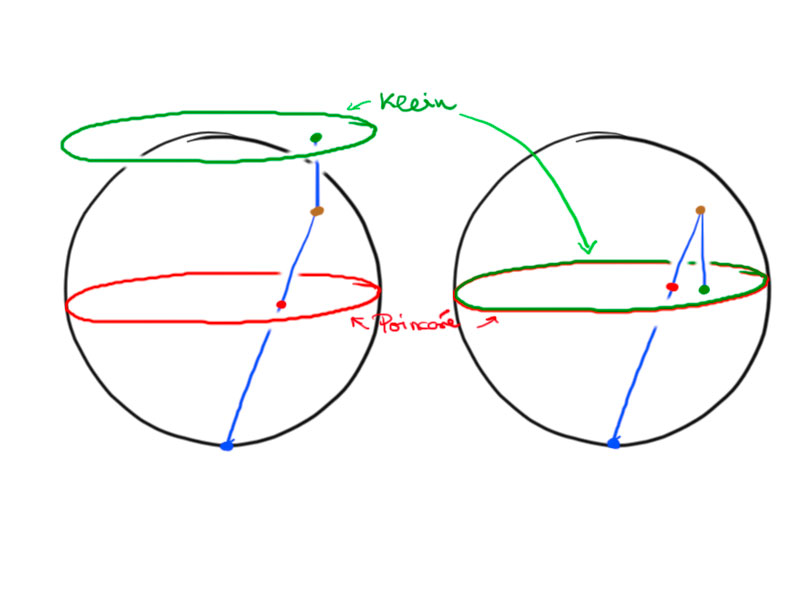
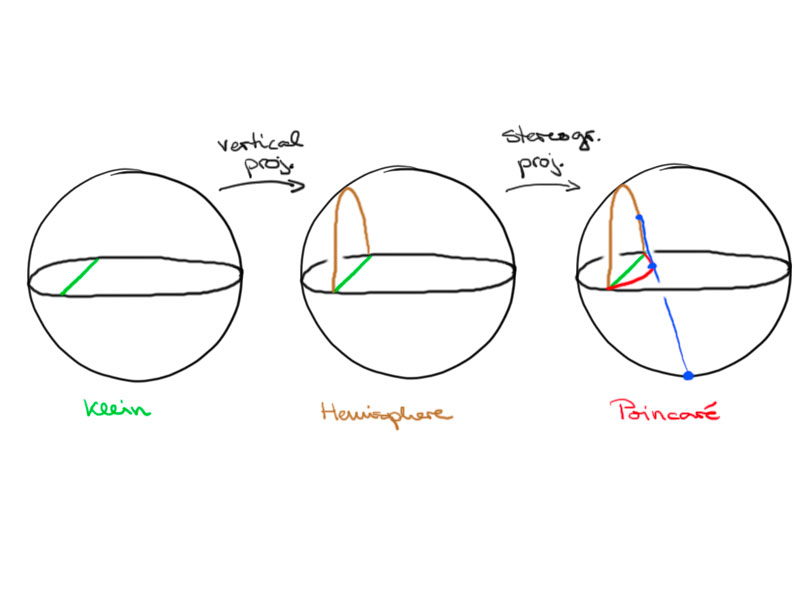
Consider the Klein and Poincaré disc and embed it in $\R^3$ at $x_3=0$ inside the unit sphere (cf. second picture).
To obtain a point in the Poincaré model from a point in the Klein model, we do the following:
- Project vertically, along $e_3$, onto the upper hemisphere.
- Use the stereographic projection from $-e_3$ (south pole) to project the upper
hemisphere back onto the disc.
Corollary
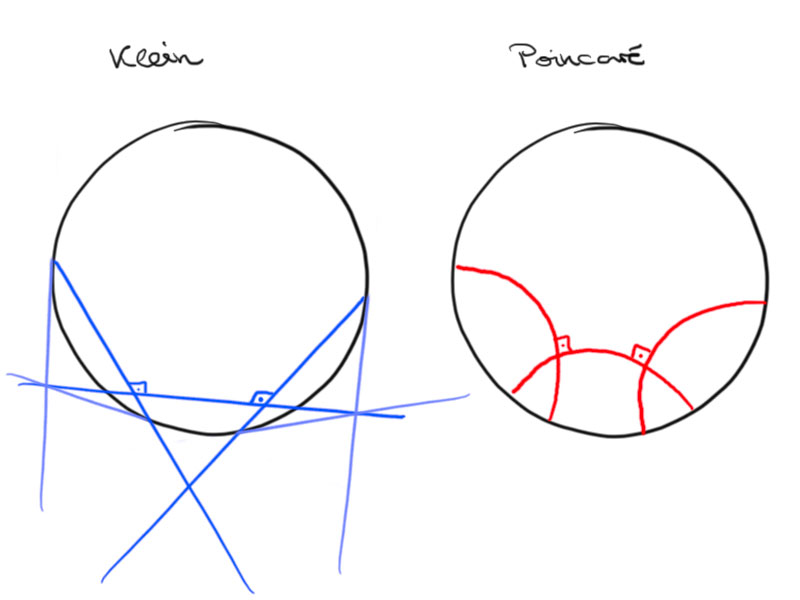
The geodesics in the Poincaré model are circular arcs (or line segments through the origin) that intersect the unit sphere/circle orthogonally.
Proof.
In the Klein model geodesics are secants. They are mapped to semicircles that intersect the boundary (the equator) orthogonally in the hemisphere.
Since the steographic projection is conformal and maps circles (or lines) to circles (or lines) the geodesics in the Poincaré disc are circular arcs that intersect the unit circle orthogonally.
Example.
For two lines construct the unique perpendicular.
Remark.
On the way we constructed another conformal model of the hyperbolic space on the hemisphere.
The Poincaré half-space(/-plane) model
Consider the following map:
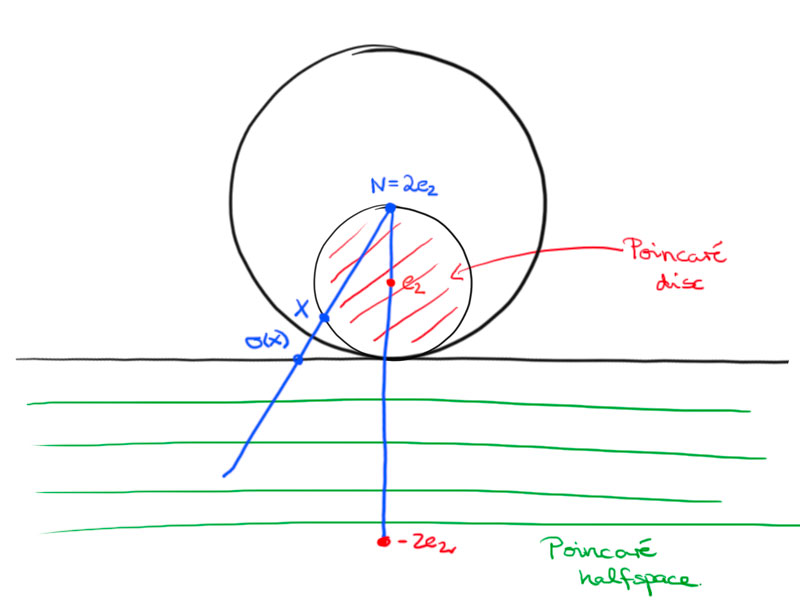
\[\sigma\colon x\mapsto\sigma(x)=2e_2+\frac4{(x-2e_2,x-2e_2)}(x-2e_2)\,.\]
We have $\sigma(S^1+e_2)=(\R\times\{0\})\cup\infty$.
Further, $\sigma(D+e_2)=H_-^2$, where $H_-^2:=\{(x,y)^{\mathrm T}\in\R^2:y<0\}$.
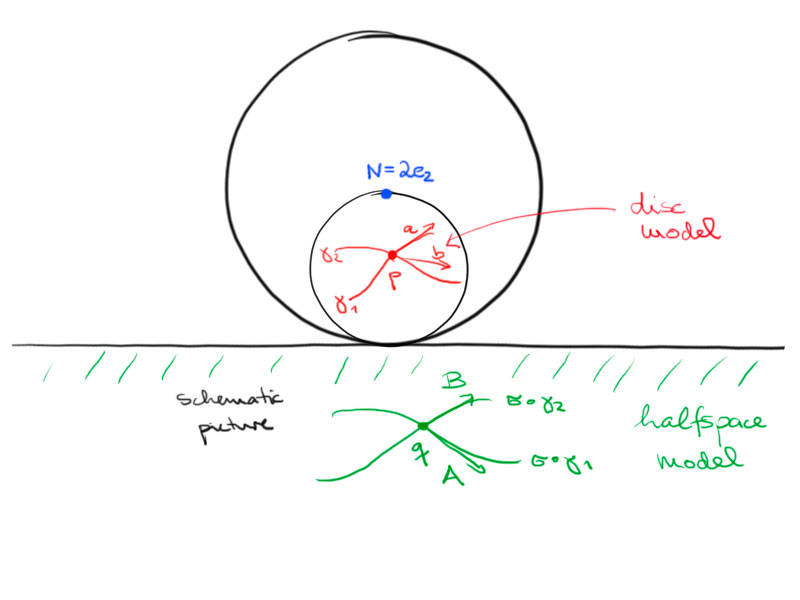
By a similar calculation as the one in the proof of conformality of the Poincaré model we can show the following:
\[(A,B)=\frac{16}{(p-e,p-e)^2)}(a,b)\]
by considering the map
\[\tilde\sigma\colon D\to H_1^2\,,\ p\mapsto2e_2+\frac4{(p-e_2,p-e_2)}(p-e_2)=\sigma(p+e_2)\,.\]
For the hyperbolic metric on the Poincaré model we had
\[g_p(a,b)=\frac4{(1-(p,p))^2}(a,b)=\frac{4(p-e_2,p-e_2)^2}{16(1-(p,p))^2}(A,B)=\frac1{q_2^2}(A,B)\,,\]
where $q=\tilde\sigma(p)$.
Definition
The upper half space $H_+^n:=\{x\in\R^n:x_n>0\}$ endowed with the Riemannian metric
\[g_q(A,B)=\frac1{q_n^2}(A,B)\]
where $q\in H_+^n$ and $A,B$ are tangent vectors to $H_+^n$ at $q$ is the \emph{Poincaré half-space model} of the hyperbolic space.
Properties:
This model is conformal, i.e. the angles between curves correspond to the Euclidean angles.
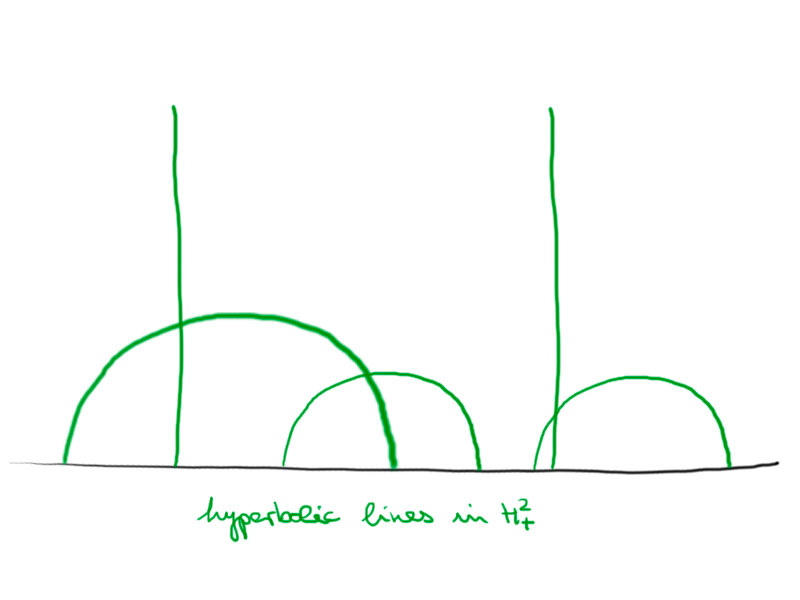
The geodesics are semi-circles or lines that intersect the boundary orthogonally.