Lengths/distances in $H_+^2$.
Two points $P_1$ and $P_2$ in the upper half-plane model either have the same $x$ coordinate or not. If they share the $x$ coordinate the geodesic through two points is a straight line. Otherwise it is a semi-circle. Let us calculate the hyperbolic distance between two points depending on the two cases.
Case 1.
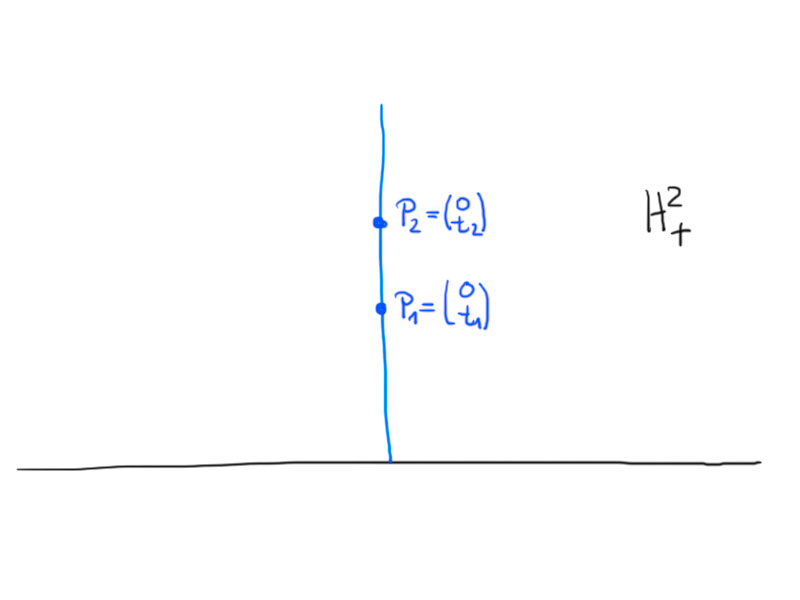
\[
\gamma\colon[t_1,t_2]\to H_+^2\,,\ \gamma(t)=\begin{pmatrix}0\\t\end{pmatrix}\,.
\]
\begin{align*}
d(p_1,p_2)&=\int_{t_1}^{t_2}\sqrt{g_{\gamma(t)}\left(\begin{pmatrix}0\\1\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\right)}\mathrm dt \\
&=\int_{t_1}^{t_2}\frac1t\sqrt{\left(\begin{pmatrix}0\\1\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\right)}\mathrm dt=\log\frac{t_2}{t_1}\,.
\end{align*}
So the length/distance only depends on the ratio $\frac{t_2}{t_1}$, not on the values.
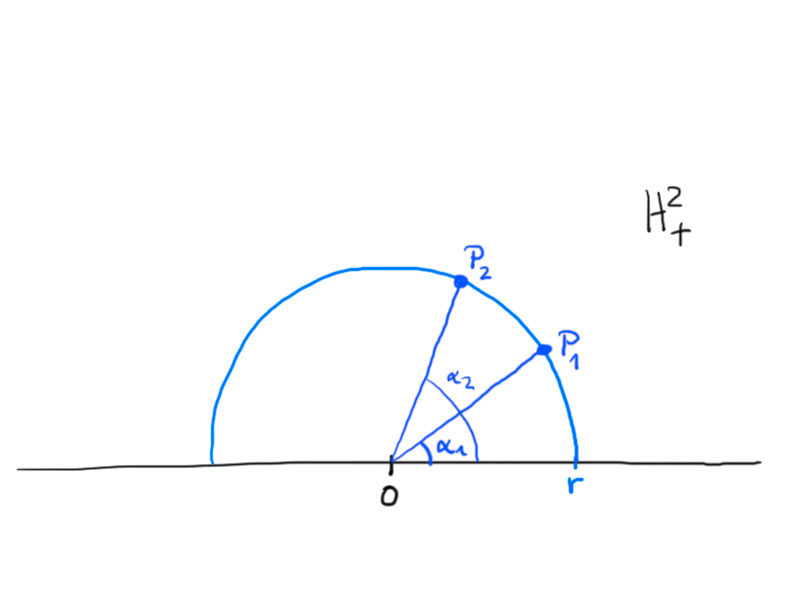
Case 2.
\begin{align*}
P_1&=r\begin{pmatrix}\cos\alpha_1\\\sin\alpha_1\end{pmatrix}&
P_2&=r\begin{pmatrix}\cos\alpha_2\\\sin\alpha_2\end{pmatrix}\,.
\end{align*}
Here,
\[\gamma\colon[\alpha_1,\alpha_2]\to H_+^2\,,\ \gamma(\alpha)=r\begin{pmatrix}\cos\alpha\\\sin\alpha\end{pmatrix}\,.\]
By this we get
\[d(p_1,p_2)=\int_{\alpha_2}^{\alpha_1}\frac1{\sin t}\mathrm dt=\left.\log\tan\frac t2\right\vert_{\alpha_1}^{\alpha_1}=\log\frac{\tan\frac{\alpha_1}2}{\tan\frac{\alpha_2}2}\,,\]
i.e. the distance depends on the angle, not on the radius.
Remrk.
The following maps are isometries of $H_+^2$:
- Horizontal translations, $\begin{pmatrix} x\\y\end{pmatrix}\mapsto\begin{pmatrix} x+c\\y\end{pmatrix}$,
- scalings, $\begin{pmatrix} x\\y\end{pmatrix}\mapsto\lambda\begin{pmatrix} x\\y\end{pmatrix}$ for $\lambda>0$.
Both transformations leave the Riemmanian metric invariant.
Proposition.
The distance in the Poincaré halfplane model $H_+^2\subset\C$ between two points $z_1$, $z_2$ is given by
\[\cosh d(z_1,z_2)-1=\frac{\lvert z_1-z_2\rvert^2}{2\operatorname{Im} z_1\operatorname{Im} z_2}\,.\]
Proof. Calculation using some trigonometric identities.
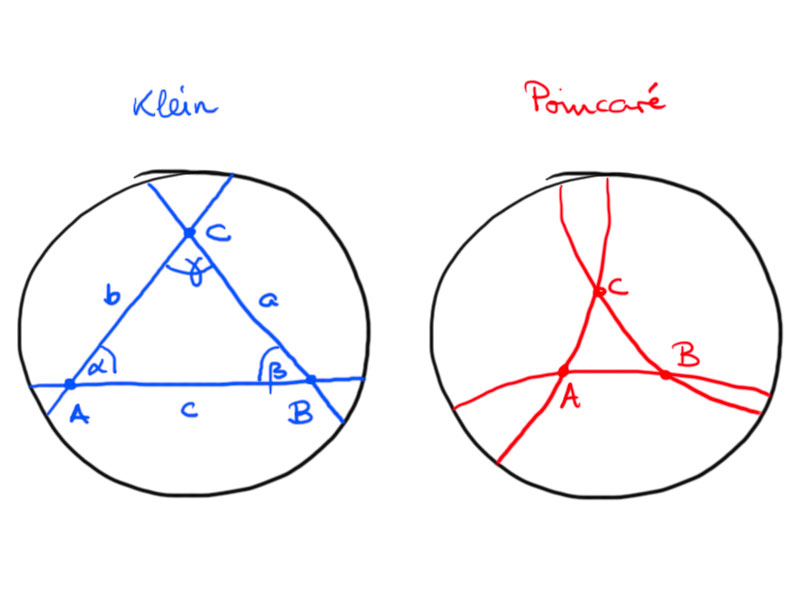
Hyperbolic triangles
Let $A$, $B$, $C$ be three points in the hyperbolic plane $H^2$ not all on one line.
Then the hyperbolic triangle is given by
\[\triangle ABC=\{\lambda A+\mu B+\nu C:\lambda,\mu,\nu>0\}\cap H^2\,.\]
The triangle defined by $A$, $B$, $C$ in the Klein model is
\[\triangle ABC=\{\lambda A+\mu B+\nu C:\lambda,\mu,\nu\geq0,\lambda+\mu+\nu=1\}\,.\]
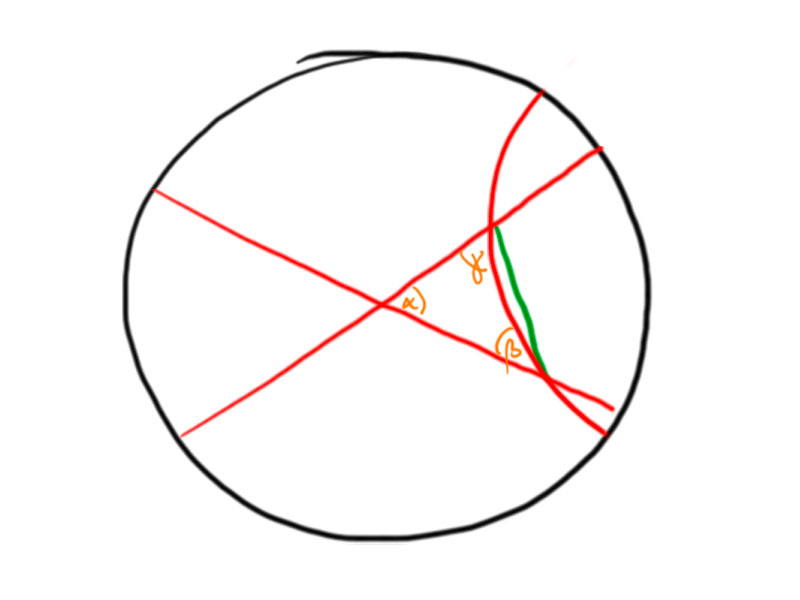
We label the vertices, angles and sides of a triangle as shown in the above picture.
Observation: $\alpha+\beta+\gamma<\pi$ for any hyperbolic triangle.
Consider a triangle in the Poincaré disc. We may use a hyperbolic motion to move $A$ to the center of the disc.
The angles between the hyperbolic lines at $B$ and $C$ are smaller than the angles of the Euclidean triangle, hence $\alpha+\beta+\gamma<\pi$.
Proposition.
For $\alpha,\beta,\gamma>0$ with $\alpha+\beta+\gamma < \pi$ there exists a hyperbolic triangle. The triangle is unique up to hyperbolic motions.
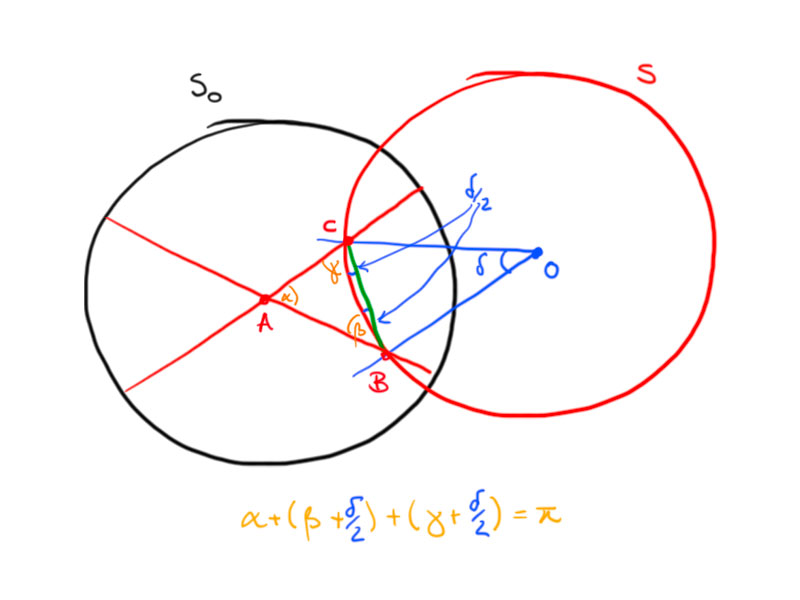
Proof. We proof the proposition by construction: Let $\delta > 0$ such that $\alpha+\beta+\gamma+\delta = \pi$. Construct a Euclidean triangle with angles $\alpha$, $\tilde\beta = \beta+\delta/2$ and $\tilde\gamma=\gamma+\delta/2$. Then construct a circle $S$ through $B$ and $C$ such that $\angle OBC=\delta$ and $O$ on the other side of $a$ than $A$. The angles between $S$ and $b$, $c$ are $\beta$ and $\gamma$, resp. Now, construct a circle $S_0$ centered in $A$ which intersects $S$ orthogonally. Scaling this construction such that the second circle has radius $1$ yields a triangle with the prescribed angles in the Poincaré model.
Theorem.
The area of a hyperbolic triangle with angles $\alpha$, $\beta$, $\gamma$ is $\pi-(\alpha+\beta+\gamma)$.
Proof.
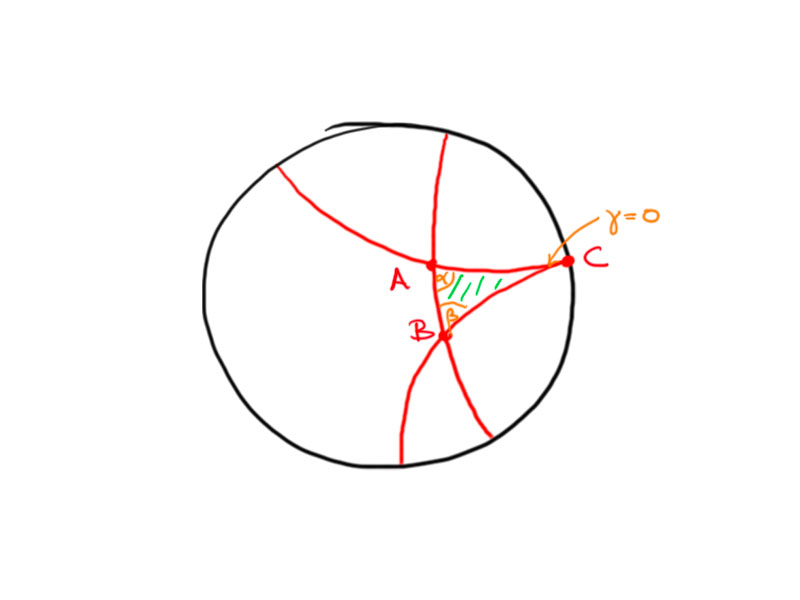
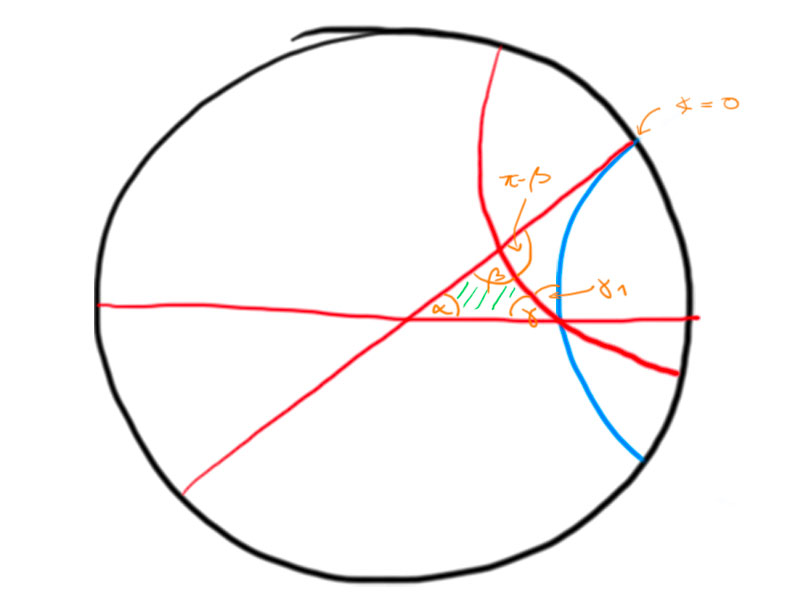
Consider a triangle with one point at infinity, i.e. on the boundary of the disc in the Poincaré model.
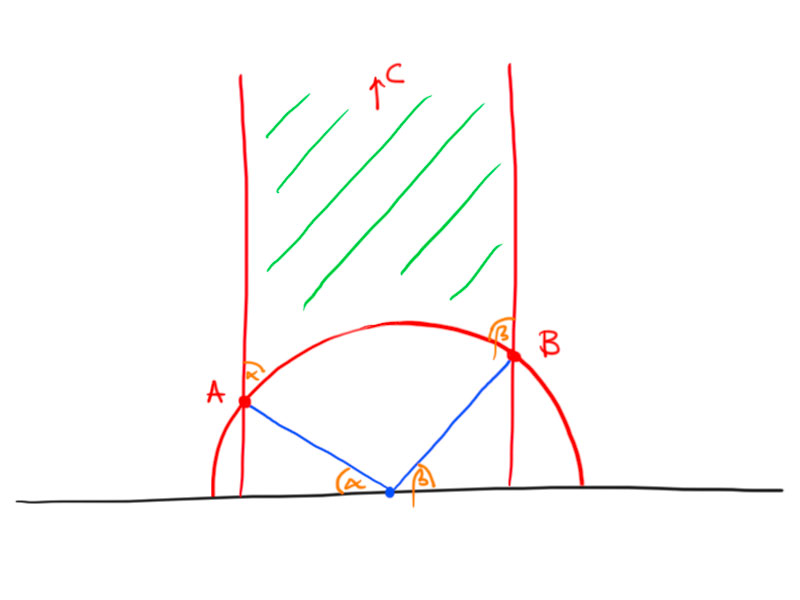
We may normalize the picture and transform it to the upper half-plane model, such that we obtain the following picture:
The area of the triangle is
\begin{align*}
T(\alpha,\beta,0)&=\int_{-\cos\alpha}^{\cos\beta}\int_{\sqrt{1-x^2}}^\infty\frac1{y^2}\mathrm dy\mathrm dx \\
&=\int_{-\cos\alpha}^{\cos\beta}-\left.\frac1y\right\vert_{\sqrt{1-x^2}}^\infty\mathrm dx \\
&=\int_{\cos(\pi-\alpha)}^{\cos\beta}\frac1{\sqrt{1-x^2}}\mathrm dx \\
&=\pi-(\alpha+\beta)\,.
\end{align*}
Now,
\begin{align*}
T(\alpha,\beta,\gamma)&=T(\alpha,\gamma+\gamma_1,0)-T(\gamma_1,\pi-\beta,0) \\
&=\pi-\alpha-\gamma-\gamma_1-(\pi-\gamma_1-\pi+\beta)\\
&=\pi-(\alpha+\beta+\gamma)\,.
\end{align*}
For given angles the hyperbolic triangle is unique. I think I talked about it, but somehow it didn’t make it into the blog. So I added it to the Theorem.