A volume form on a discrete surface $M$ is a 2-form $dA$ such that $\textrm{vol}(\varphi):=dA(\varphi)>0$ for all faces $\varphi \in F$. The interpretation is that a volume form assign an area $\textrm{vol}(\varphi)$ to each face $\varphi$. The total area of $M$ is then defined as
$\displaystyle \textrm{vol}(M):=\int_M dA = \sum_{\varphi \in F} \textrm{vol}(\varphi)$
Given a volume form $dA$, we can define the integral of a dual function $f\in \Omega_0(M^*)$:
$\displaystyle \int_M f :=\int_M f\,dA= \sum_{\varphi \in F} f|_\varphi\,\textrm{vol}(\varphi)$.
Here we have used the notation
$f|_\varphi := f(\varphi)$
for the evaluation of dual 0-forms on faces (recall they are to be viewed as functions that are constant on faces).
We can use this to make $\Omega_0(M^*)$ into a euclidean vector-space by defining a scalar product
$\displaystyle \langle \! \langle f,g \rangle \! \rangle =\int_M fg\, \,dA$.
One way to view such a scalar product is that it defines an isomorphism $\star_2^{-1}$ into the dual space:
$\star_2^{-1}: \Omega_0(M^*) \rightarrow \Omega_0(M^*)^*=\Omega_2(M)$
$\displaystyle \langle \star_2^{-1}(f), g \rangle := \langle \! \langle f,g \rangle \! \rangle= \int_M gf \, dA$.
Thus $\star_2^{-1}(f) = f \, \sigma$. Setting $\star_2^{-1}(f)=:\tau$ this implies $\tau(\varphi)= \star_2(\varphi) \sigma(\varphi)$ for all $\varphi \in F$ or
$\displaystyle (\star_2 \tau)|_\varphi = \frac{1}{\textrm{vol}(\varphi)} \int_\varphi \tau$
Similarly, a volume form on $M^*$ allows to integrate functions $f \in \Omega_0(M)$, now seen as functions that are constant on each dual cell. Then we also have a euclidean scalar product on $\Omega_0(M)$. Now it seems unreasonable to choose $\sigma$ and $\sigma^*$ in a completely independent way. For example, a natural demand seems to be that $M$ and $M^*$ have the same area:
$\textrm{vol}(M^*) = \textrm{vol}(M)$.
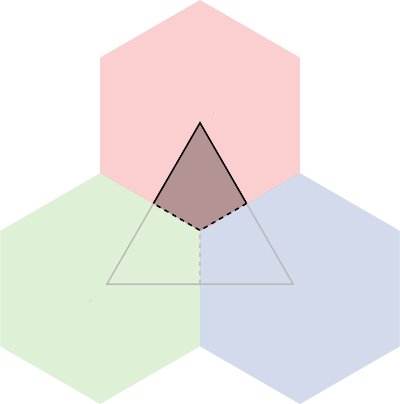
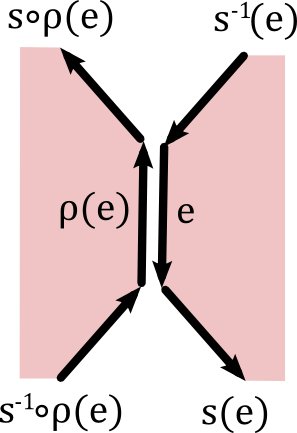
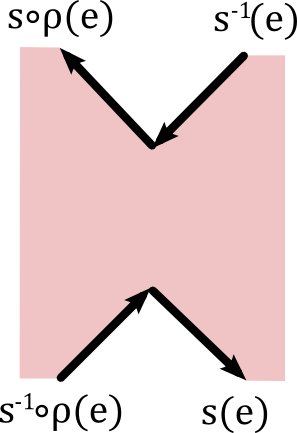
We can ensure this and other natural properties by deriving both $\sigma$ and $\sigma^*$ from a volume-form on the kite complex of $M$. This is a discrete surface that kind of mediates between $M$ and $M^*$. The kite complex has vertices at the vertices of $M$, the vertices of $M^*$ and the “centers” of the edges of $M$ (understood combinatorially). Its faces (the kites) are all quadrilaterals and correspond to the intersections of faces of $M$ (the so-called primal faces) with faces of $M^*$ (the so-called dual faces). In the picture below, the triangle is a primal face and is the union of three kites. Each of the three dual faces is a union of six kites.
It is a nice exercise to construct the Kite complex as a discrete surface $M^K=(E^K,s^K,\rho^K)$. What is clear is that (up to a canonical bijection) the set of faces of $M^K$ is
$F^K = \{(v,\varphi)\in V \times F \,|\, v \cap \varphi \neq \emptyset\}$.
Here the intersection of $v$ and $\varphi$ is to be understood as subsets of $E$.