I put the configurations I showed on the projector online:
You may move the points around to see how the configuration changes.
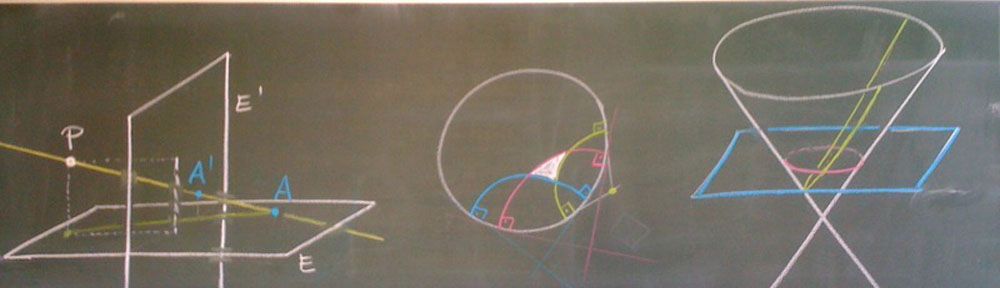
I put the configurations I showed on the projector online:
You may move the points around to see how the configuration changes.
Consider the linear projection map for the homogeneous coordinates of the central projection described in the first lecture. What are the images of the points on the line $l_\infty$ if we assign homogeneous coordinates $\svector{b_1\\b_2\\0}$ with $b_1 \neq 0$ to the points on the line?
How can you construct the perspective image of the first square given the position of the chessboard, your position (the “eye” point), and the position of the plane projected onto? The construction of the other “squares” is described in the first lecture.