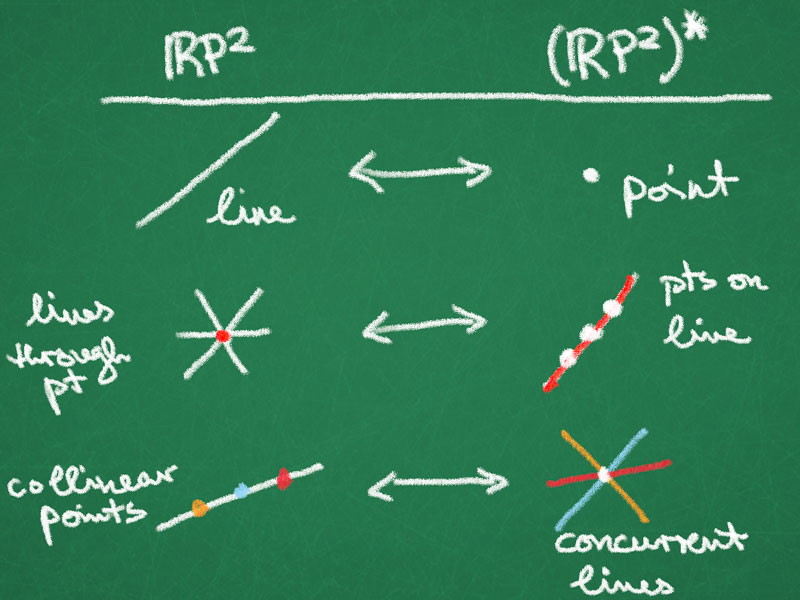
Note If a conic in $\mathbb{R}P^{2}$ contains a line, then it is degenerate.
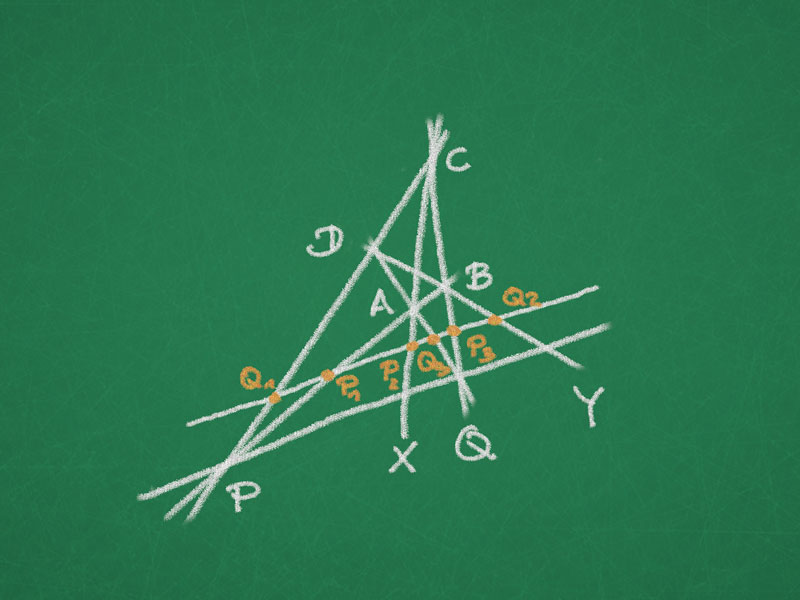
Theorem. Through five points $P_{1},P_{2},P_{3},P_{4},P_{5} \in \mathbb{R}P^{2}$ there exists a conic in $\mathbb{R}P^{2}$.
$i)$ If no four points lie on a line, then the conic is unique.
$ii)$ If no three lie on one line (five points in general position), then the conic is non-degenerate.
Lemma. If a conic contains three collinear points, then it contains the line through these points. Continue reading