Theorem (Hyperbolic Pythagoras).
Let $\triangle ABC$ be a hyperbolic triangle with angles $\alpha$, $\beta$ and $\gamma=\frac\pi2$.
Then the lengths of the edges $a$, $b$ and $c$ satisfy
\[\cosh c=\cosh a\cdot\cosh b\,.\]
Proof.
We calculate the length in the upper half-plane model after normalizing the triangle to the following:
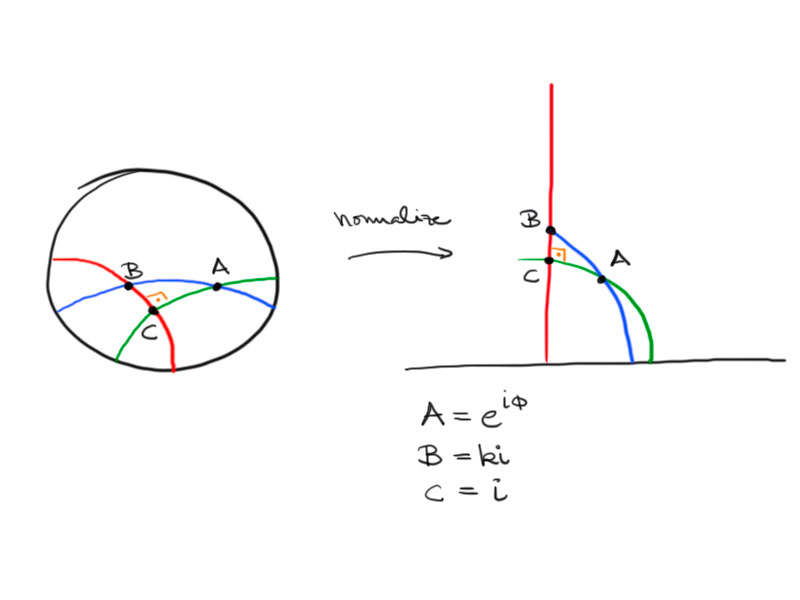
We use the formula derived for the hyperbolic distance in the upper half-plane using complex variables:
\[
\cosh d(z_1,z_2)-1
=\frac{\lvert z_1-z_2\rvert^2}{2\operatorname{Im}z_1\operatorname{Im}z_2}\,,
\]
So for the length of the edges of the triangle we obtain:
\begin{align*}
\cosh a&=1+\frac{\lvert B-C\rvert^2}{2\operatorname{Im}B\operatorname{Im}C}\\
&=1+\frac{(k-1)^2}{2k}=\frac{k^2+1}{2k}\\
\cosh c&=1+\frac{\lvert\mathrm e^{\mathrm i\phi}-k\mathrm i\rvert^2}{2k\sin\phi}\\
&=1+\frac{\left(\mathrm e^{\mathrm i\phi}-k\mathrm i\right)\left(\mathrm e^{-\mathrm i\phi}+k\mathrm i\right)}{2k\sin\phi}\\
&=1+\frac{k^2+1-2k\sin\phi}{2k\sin\phi}\\
&=\frac{k^2+1}{2k\sin\phi}\\
\cosh b&=\frac{1^2+1}{2\cdot1\cdot\sin\phi}\\
&=\frac1{\sin\phi}\,.
\end{align*}
This calculation implies the required equality.
What is the relation of hyperbolic and Euclidean triangles?
Looking at “small” hyperbolic triangles (i.e. triangles with small edge lengths and area) hyperbolic triangles behave similar to Euclidean triangles.
If the area is very small, then the sum of its interior angles is almost $\pi$.
The hyperbolic Pathagoras’ Theorem becomes the Euclidean Pythagoras’ Theorem for small edge lengths:
The Taylor series for $\cosh$ is $\cosh x=\sum\frac{f^{(k)}(0)}{k!}x^k=1+\frac12x^2+\dotsb$.
Thus $\cosh c=\cosh a\cdot\cosh b$ becomes
\[1+\frac{c^2}2+\dotsb=\left(1+\frac{a^2}2+\dotsb\right)\left(1+\frac{b^2}2+\dotsb\right)\,,\]
hence
\[1+\frac{c^2}2=1+\frac{a^2}2+\frac{b^2}2+\underbrace{\frac{a^2b^2}4+\dotsb}_{\approx0}\]
which gets $c^2=a^2+b^2$ for small $a$, $b$ and $c$.
Hyperbolic motions in $H_+^2$
Consider the following maps:
\[g\colon\hat\C\to\hat\C\,,\ z\mapsto\frac{az+b}{cz+d}\,,\]
where $ad-bc>0$ and $a,b,c,d\in\R$.
Here, $g$ maps $\infty$ to $\frac ac$ and $-\frac dc$ to $\infty$.
Also,
\[\tilde g\colon\hat\C\to\hat\C\,,\ z\mapsto\frac{-a\bar z+b}{-c\bar z+d}\,.\]
- The maps $g$ and $\tilde g$ are bijective (the inverse is just the transformation corresponding to $\begin{pmatrix}a&b\\c&d\end{pmatrix}^{-1}$).
- These maps preserve the upper half-plane:
We have
\begin{align*}
\operatorname{Im}g(z)
&=\frac1{2\mathrm i}\left(\frac{az+b}{cz+d}-\frac{a\bar z+b}{c\bar z+d}\right)\\
&=\frac1{2\mathrm i\lvert cz+d\rvert^2}\left(ac\lvert z\rvert^2+adz-ac\lvert z\rvert^2-ad\bar z+bc\bar z+bd-bcz-bd\right)\\
&=\frac{ad-bc}{2\mathrm i\lvert cz+d\rvert^2}(z-\bar z)\\
&=\frac{ad-bc}{\lvert cz+d\rvert^2}\operatorname{Im}z>0\,.
\end{align*}
Similarly for $\tilde g$.
- These maps are isometries:
\begin{align*}
\frac{\lvert g(z_1)-g(z_2)\rvert^2}{2\operatorname{Im}g(z_1)\operatorname{Im}g(z_2)}
&=\frac{\lvert cz_1+d\rvert^2\lvert cz_2+d\rvert^2}{(ad-bc)^2}\frac1{\operatorname{Im}z_1\operatorname{Im}z_2}\frac{(ad-bc)^2\lvert z_2-z_1\rvert^2}{2\lvert cz_1+d\rvert^2\lvert cz_2+d\rvert^2}\\
&=\frac{\lvert z_1-z_2\rvert^2}{2\operatorname{Im} z_1\operatorname{Im}z_2}\,.
\end{align*}
Again, a similar calculation for $\tilde g$ yields that $\tilde g$ is also an isometry.
- Hyperbolic lines are mapped to hyperbolic lines.
Theorem.
An arbitrary hyperbolic isometry of $H_+^2$ is of the form
\[z\mapsto\frac{az+b}{cz+d}\quad\text{or}\quad z\mapsto\frac{-a\bar z+b}{-c\bar z+d}\,,\]
where, again, $ad-bc>0$ and $a,b,c,d\in\R$.
Proof.
Let $\phi\colon H_+^2\to H_+^2$ be an isometry. We can construct a map $g$ which is one of the following, such that $g\circ\phi$ maps the imaginary axis onto itself and $g\circ\phi(\mathrm i)=\mathrm i$ and $g\circ\phi((0,\mathrm i))=(0,\mathrm i)$:
- $z\mapsto\frac{z-u}v$ with $\phi(\mathrm i)=u+\mathrm i v$,
- $z\mapsto\frac v{\bar z-u}$,
- $z\mapsto\alpha\frac{z-x}{z-y}$ where $\phi(0)=x$, $\phi(\infty)=y$.
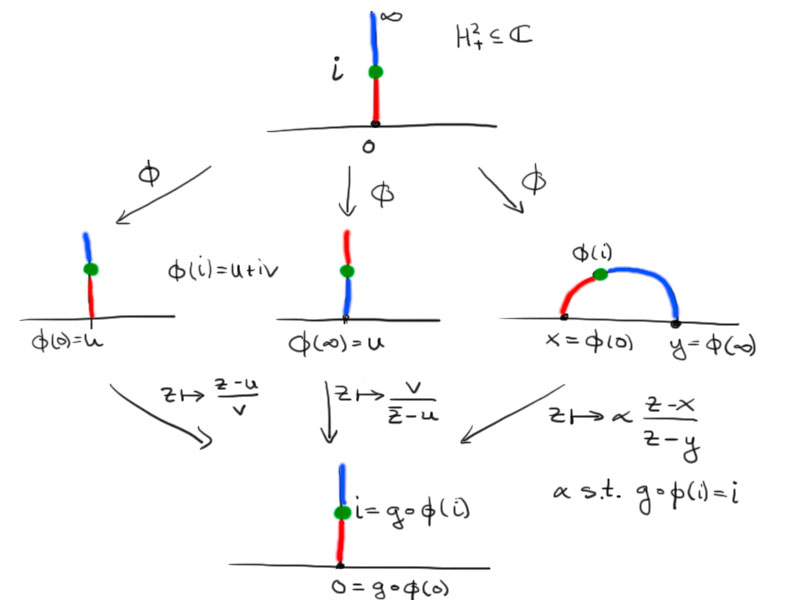
Then $g\circ\phi$ is an isometry, since $g$ and $\phi$ are. Further $g\circ\phi$ is the identity on the imaginary axis, as it is isometric and maps the imaginary axis onto itself preserving the intervals $(0,\mathrm i)$ and $(\mathrm i,\infty)$.
Now consider $x+\mathrm i y$ with $g\circ\phi(x+\mathrm i y)=u+\mathrm i v$.
We have $d(k\mathrm i,x+\mathrm i y)=d(g\circ\phi(k\mathrm i),u+\mathrm i v)=d(k\mathrm i,u+\mathrm i v)$ for all $k\in\R^+$.
Thus
\[\frac{\lvert k\mathrm i-(x+\mathrm i y)\rvert^2}{2ky}=\frac{\lvert k\mathrm i-(u+\mathrm i v)\rvert^2}{2kv}\]
and hence
\[(x^2+(k-y)^2)v=(u^2+(v-k)^2)y\]
for all $k$.
This implies $y=v$ and $u=\pm x$.
So $g\circ\phi$ is either the identity or it the reflection with respect to the imaginary axis, $z\mapsto-\bar z$.
As $\phi=g^{-1}\circ g\circ\phi$, $\phi$ is of the given type.