Quadrics
Definition. Let $q$ be a quadratic form on $\mathbb{R}^n$ or $\mathbb{C}^n$. Then the corresponding quadric is $Q = \{[v] \in \RP^n \mid q(v) =0\}$
A conic is a quadric in $\RP^2$.
How many indefinite non-degenerate quadratic forms exists in $\mathbb{R}^{n+1}$ up to change a basis?
Classification by the signature: (+++..+), (+++..+ -), …, (+ – …-), (- – – ..-), should be indefinite $\Rightarrow$ n indefinite quadrtic forms (+++..+ -), … , (+ – …-).
The number of non-empty non-degenerate quadrics in $\mathbb{R}P^n$ is $\lceil \frac{n}{2} \rceil$
Example
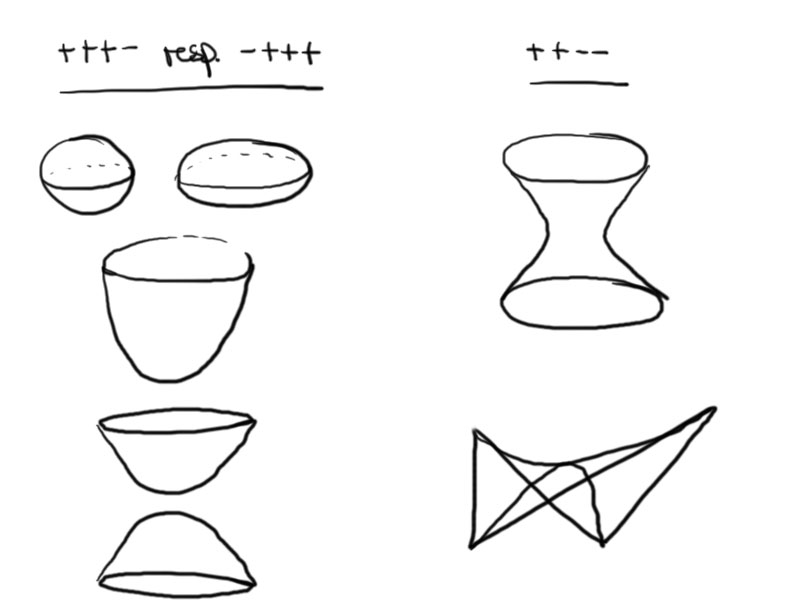
$n=2$: In $\RP^2$ there exist only one indefinite non-degenerate quadric/conic up to projective transformations. It has signature ( + + – ) resp. ( – – +).
$n=3$: In $\RP^3$ there exist $\lceil \tfrac32 \rceil = 2$ different quadrics up to projective transformations:
- (+ + + – ), ( – – – +), $Q_1 = \{[v] \in \mathbb{R}P^3 \mid v_1^2 + v_2^2 + v_3^2 – v_4^2 = 0 \}$
- ( + + – – ), ( – – – +), $Q_2 = \{[v] \in \mathbb{R}P^3 \mid v_1^2 + v_2^2 – v_3^2 – v_4^2 = 0 \}$
1. is a unit sphere (or ellipse, paraboloid or 2-sheeted hyperboloid) depending on the choice of affine coordinate. To obtain a sphere as affine image of the quadric we can choose the affine coordinates $u_1 = \frac{v_1}{v_4}$, $u_2 = \frac{v_2}{v_4}$, and $u_3 = \frac{v_3}{v_4}$.
2. is one-sheeted hyperboloid or hyperbolic paraboloid.
Degenerate Quadratic forms/quadrics.
Let b be a degenerate bilinear form. Then the space $\{ u \in U \mid b(u, v) = 0 \forall v \in V \} = \ker(b) $ is a subspace of $V$. Consider a subspace $U_1 \subset V$ such that $V = \ker(b) \oplus U_1$, then $b\mid_{U_1}$ defines a non-degenerate quadric $Q_1$ in $P(U_1)$. The quadric $Q$ defined by $b$ is the union of lines through points in the non-degenerate quadric $Q_1$ defined by $b|_{U_1}$ and points in $ P(\ker(b))$ if $Q_1 \neq \emptyset$ (see Exercise 8.1).
Example of degenerate conic.
Consider the following bilinear form in $\mathbb{R}P^2$:
\[
b (\begin{pmatrix} x_1\\ x_2\\x_3\end{pmatrix} , \begin{pmatrix} x_1\\ x_2\\ x_3\end{pmatrix}) = {x_1}^2 – {x_2}^2.
\]
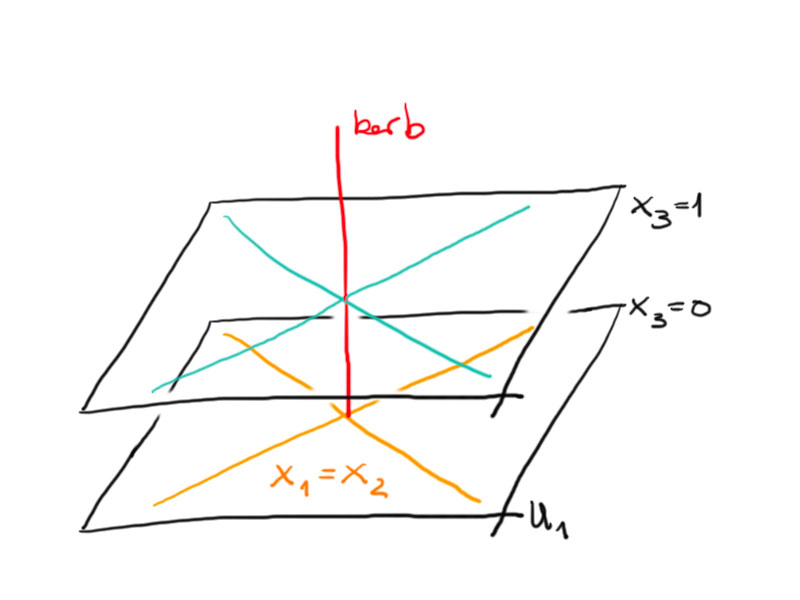
Then $\ker (b) = span \{e_3\}$ and $\mathbb{R}^3 = \ker(b) \oplus \underbrace {span\{e_1, e_2\} }_{U_1}$. Projectively, $P(\ker(b))$ is a point and the quadric defined by $b|_{U_1}$ in $P(U_1)$ consists of two points. So the degenerate/singular conic definined by $b$ in $\RP^2$ consists of two crossing lines.
Proposition. A non-degenerate non-empty quadric $Q \subset \RP^n$ determines the corresponding bilinear form up to a non-zero scalar multiple.
Proof. Let $b$ and $\tilde b$ be two linear forms defining $Q$. Consider an orthonormal basis w.r.t. $b$, i.e. $\{ e_1 .. e_p, f_1 .. f_q \} $, such that:
- $b(e_i, e_i) = 1$ for all $i = 1, \ldots, p$;
- $b(f_j, f_j) = -1$ for all $j = 1, \ldots, q$; and
- $b(e_i, e_k) = b(f_j, f_l) = b(e_i, f_j) = 0$ for all
$i, k = 1, \ldots, p$ with $i \neq k$ and
$j, l = 1, \ldots, q$ with $j \neq l$.
Consider the vectors $e_i \pm f_j$. Then
\begin{align*}
& b( e_i \pm f_j, e_i \pm f_j) = \underbrace{b(e_i, e_i)}_{=1} \pm \underbrace{2b(e_i, f_j)}_{=0} + \underbrace{b( f_j, f_j)}_{-1} = 0 \\
\Rightarrow& 0 = \tilde b( e_i \pm f_j, e_i \pm f_j) = \tilde b(e_i, e_i) \pm \tilde 2b(e_i, f_j) + \tilde b ( f_j, f_j)\\
\Leftrightarrow& \pm 2 \tilde b (e_i, f_j) = – \tilde b(e_i, e_i) – \tilde b(f_j, f_j) \\
\Rightarrow& \tilde b (e_i, f_j) = 0 \\
\Rightarrow& \tilde b(e_i, e_i) = – \tilde b (f_j, f_j).
\end{align*}
So setting $\tilde b (e_1, e_1) = \lambda \neq 0$ implies that $\tilde b(e_i, e_i) = \lambda$ for all $i = 1, \ldots, p$ and $\tilde b(f_j, f_j) = – \lambda$ for all $j = 1, \ldots, q$.
Orthogonal Transformations
Definition. Let $b$ be a non-degenerate symmetric bilinear form on $\mathbb{R}^{n+1}$. Then $F: \mathbb{R}^{n+1} \rightarrow \mathbb{R}^{n+1} $ is orthogonal (wrt. $b$) if $ b(F(v), F(w)) = b(v,w) \forall v,w \in \mathbb{R}^{n+1}$.
The group of orthogonal transformations for a bilinear form of signature $(p, q)$ with $p+q = n+1$ is denoted by $ O(p,q)$. If $q=0$ we obtain the “usual” group of orthogonal transformations $O(n+1) = O(n+1, 0)$
If $Q \subset \RP^n$ is a non-degenerate quadric defined by $b$ and $F: \mathbb{R}^{n+1} \rightarrow \mathbb{R}^{n+1} $ is an orthogonal transformation, then the map $f: \mathbb{R}P^n \rightarrow \mathbb{R}P^n$ with $[x] \mapsto f([x]) = [F(x)]$ maps the quadric onto itself: $f(Q) = Q$.
Proposition. If the signature of a non-degenerate quadric $Q$ is $(p,q)$ with $p \neq q$ and $p \neq 0 \neq q$, then any projective transformation with $ f(Q) = Q$ is induced by an orthogonal transformation $F$ w.r.t. $b$ that defines $Q$.
Proof. Let $b$ be the bilinear form defining $Q$ and $F$ the linear transformation defining the projective transformation $f$. Then $\tilde b(v,w):= b(F(v), F(w))$ is another bilinear form defining $Q$.
According to the previous proposition there exists $\lambda \neq 0$ such that
\[b=\lambda \tilde b.\]
If $\lambda > 0 $ then $\frac{1}{\sqrt \lambda} F$ is an orthogonal transformation, since $ b( \frac{1}{\sqrt \lambda} F(v), \frac{1}{\sqrt \lambda} F(w)) = \frac{1}{\lambda} b (F(v), F(w)) = \frac{1}{\lambda}\tilde b (v,w) = b(v,w)$.
So we need to show that $\lambda > 0$.
If $\{ e_1, \ldots, e_{n+1}\}$ is an orthogonal basis of $\mathbb{R}^{n+1}$ w.r.t. $b$ then $\{F(e_1), \ldots, F(e_{n+1}\}$ is also orthogonal with
- If $b(e_i, e_i) = 1$ then $\tilde b(e_i, e_i) = \lambda$
- $b(e_i, e_i) = -1 \Rightarrow \tilde b(e_i, e_j) = – \lambda$.
But the signature is invariant w.r.t. to change of basis (i.e. w.r.t. F). So since $ p \neq q$ we have that the $\lambda $ is positive. $\square$
If $p = q$ (neutral signature), for example $p=q=2$ for a quadric in $\RP^3$, then there exists a projective transformation preserving the quadric not induced by an orthogonal transformation. Let $b(x,x) = {x_1}^2 + {x_2}^2 – {x_3}^2 – {x_4}^2$. Then the map:
\[
f : \RP^3 \rightarrow \RP^3 ,
\sqvector{x_1\\x_2\\x_3\\x_4}
\mapsto
\sqvector{x_3\\x_4\\x_1\\x_2}
\]
yields $b(F(v), F(w)) = – b (x,x) = {x_3}^2 + {x_4}^2 – {x_1}^2 – {x_2}^2$. So $f$ preserves the quadric but it is not induced by an orthogonal transformation $F$.