It is well known that $\mathbb{C} \cong \mathbb{R}^2$ with
\[
z = x + y i \leftrightarrow (x,y) \leftrightarrow \begin{pmatrix}
x & – y
\\
y & x
\end{pmatrix}
=
\begin{pmatrix}
x & – y
\\
\overline{y} & \overline{x}
\end{pmatrix}
\]
Note that the multiplication rule in $\mathbb{C}$ comes from the matrix multiplication in $\mathbb{R}^{2 \times 2}$ with
\[
(x + y i)(x’ + y’ i) = (xx’ – yy’) + (xy’ + yx’)i
\]
for some $x,y,x’,y’ \in \mathbb{R}$. Of course other known operations for $x,y \in \mathbb{R}, z := x + yi$ are:
\begin{gather*}
\overline{z} = \overline{x + yi} = x – yi
\\
|z|^2 = z \overline{z} = x^2 + y^2 \in \mathbb{R}^{\ge 0}
\\
z^{-1} = \frac{\overline{z}}{|z|^2}
\\
\overline{z} = z \Leftrightarrow |z| = 1 \Leftrightarrow z \in \mathbb{S} \Leftrightarrow \begin{pmatrix}
x & – y
\\
y & x
\end{pmatrix} \in \text{SO}_2 = \{\text{special orthogonal}\}
\end{gather*}
Now consider a pair of complex numbers which will be called quaternion. Denote $\mathbb{H}$ as the set of all quaternions (named after Hamilton). Then $\mathbb{H} \cong \mathbb{C}^2 \cong \mathbb{R}^4$ with
\[
q = z + w i \leftrightarrow (z,w) \leftrightarrow
\begin{pmatrix}
z & – w
\\
\overline{w} & \overline{z}
\end{pmatrix}
\]
Accordingly we get the following rules for $z,w, z’, w’ \in \mathbb{C}, q := z + wj$:
\begin{gather*}
(z + w j)(z’ + w’ j) = (zz’ – w \overline{w’}) + (zw’ + w \overline{z’})j
\\
\overline{q} = \overline{z + wj} = \overline{z} – wj
\\
|q|^2 = q \overline{q} = |z|^2 + |w|^2 \in \mathbb{R}^{\ge 0}
\\
q^{-1} = \frac{\overline{q}}{|q|^2}
\\
\overline{q} = q \Leftrightarrow |q| = 1 \Leftrightarrow q \in \mathbb{S} \Leftrightarrow \begin{pmatrix}
z & – w
\\
\overline{w} & \overline{z}
\end{pmatrix} \in \text{SU} \cong \text{SU}_2
\end{gather*}
May think of it in a constructive way:
- Start with $\mathbb{R}$ (we have $(x \mapsto \overline{x}) = \text{id}$, $\cdot$ is commutative and associative)
- Double to get $\mathbb{C}$ (we lose $(x \mapsto \overline{x}) = \text{id}$)
- Double to get $\mathbb{H}$ (we lose commutativity of multiplication)
- Double to get the octonions $\mathbb{O}$ with $\mathbb{O} \cong \mathbb{H}^2$ (we lose the associativity, too)
As a basis for $\mathbb{H}$ over $\mathbb{R}$ we can choose $\{1 , i, j, k\}$ with $k := ij$. We get
\begin{gather*}
i^2 = j^2 = k^2 = ijk = -1
\\
ij = -ji = k
\\
jk = -kj = i
\\
ki = -ik = j
\end{gather*}
The set $\{ \pm 1, \pm i, \pm j, \pm k\}$ forms a group $Q_8$, called the quaternion group of order 8.
Then we can write $q \in \mathbb{H}$ as
\[
q = t + xi + yj + zk = t + p \text{ for some } t,x,y,z \in \mathbb{R}
\]
where $p = xi + yj + zk$ is a pure (imaginary) quaternion. We denote $\text{Im}(q) := p \in \mathbb{R}^3, \text{Re}(q) := t \in \mathbb{R}$.
Identify the pure quaternions $\text{Im} \mathbb{H} := \text{span}\{ i,j,k\}$ with $\mathbb{R}$ via
\[
q \longleftrightarrow
\begin{pmatrix}
t & x & y & z
\\
-x & t & -z & y
\\
-y & z & t & -x
\\
-z & -y & x & t
\end{pmatrix}
\]
The following rules holds $t,x,y,z,t’ \in \mathbb{R},p,p’ \in \text{Im} \mathbb{H}$ with $p = xi + yj + zk$ and $q := t + p, q’ := t’ + p’$:
\begin{gather*}
\overline{q} = \overline{t + p} = t – p
\\
q \overline{q} = t^2 + x^2 + y^2 + z^2 = t^2 + |p|^2
\\
\overline{p} = -p
\\
( \overline{q} = q \Leftrightarrow t = 0 \Leftrightarrow q \in \text{Im} \mathbb{H} )
\\
q q’ = (t+p)(t’+p’) = (tt’ – p \cdot p’) + ( tp’ + t’p + p \times p’)
\end{gather*}
where $p \cdot p’$ is the common scalar product and $p \times p’$ the vector product on $\mathbb{R}^3$. In particular
\[
p p’ = – \underbrace{p \cdot p’}_{\in \mathbb{R}} + \underbrace{p \times p’}_{\in \mathbb{R}^3}, \quad – p \cdot p’ = \text{Re}(pp’), p \times p’ = \text{Im}(p p’)
\]
Any 2-dim subspace in $\mathbb{H}$ including 1 behaves like $\mathbb{C}$ (closed under the commutative multiplication). That is, given any unit pure quaternion $u \in \mathbb{S}^2 = \mathbb{R}^3 \cap \mathbb{S}^3$ the set $\{1,u\}$ spans such a 2-plane
\begin{gather*}
(x+ yu)(x’+y’u) = (xx’ – yy’) + (xy’ + yx’) u
\\
u^2 = -1
\end{gather*}
A non-real quaternion $q$ commutes only with elements of $\text{span}\{1,u\}$. $\mathbb{R} \subset \mathbb{H}$ is called the center of $\mathbb{H}$ (because the reals commute with everything). Analog to the complex setting we have $e^{\theta i} = \cos \theta + \sin \theta i$ and define
\[
e^{\theta u} := \cos \theta + \sin \theta u \quad \forall u \in \mathbb{S}^2, \theta \in \mathbb{R}
\]
For $q = t + p = t + \theta u$ we get
\[
e^q = e^t(e^{\theta u}) = e^t \cos \theta + (e^t \sin \theta)u
\]
and $e^{\theta u} \in \mathbb{S}^3$ (unit quaternions).
Claim: Any unit quaternion can be written as $e^{\theta u}$ for some $\theta \in [0, \pi], u \in \mathbb{S}^2$ (unit pure).
Indeed $\cos \theta = \text{Re}(q) \in [-1,1]$ determines $\theta \in [0,\pi]$ uniquely. Then $u = \frac{\text{Im}(q)}{|\text{Im}(q)|} = \frac{\text{Im}(q)}{\sin \theta}$ determines $u$. (Except for $\theta \in \{0,\pi\}$ since $1 = e^{0u}, -1 = e^{\pi u} \forall u \in \mathbb{S}^2$.)
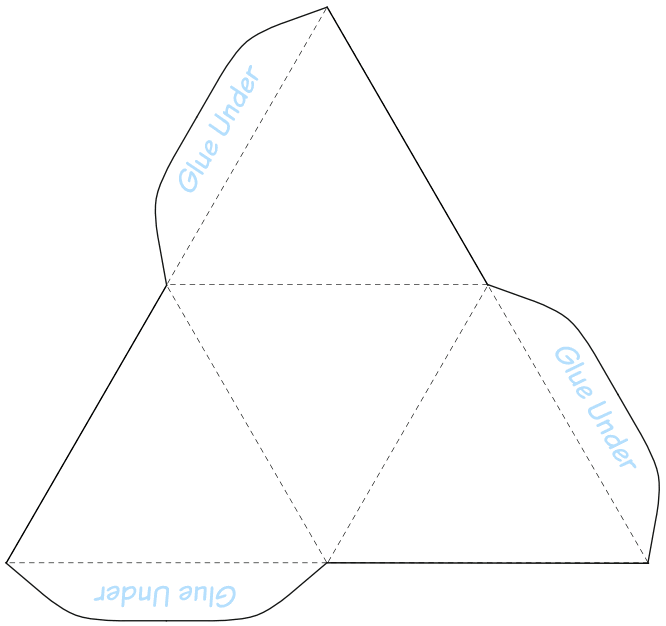The tetrahedron has the symmetry group $*233$, with rotation subgroup $233$.
