In the last tutorial we constructed certain minimal surfaces in hyperbolic space. These hyperbolic helicoids were generated by a 1-parameter family of geodesics: while moving on a geodesic – the axis of the helicoid – another geodesic perpendicular to the axis was rotated with constant speed. It turns out that the very same procedure applied to the 3-sphere yields minimal surfaces, too.
Actually the geodesics in the 3-sphere are great circles, i.e. the intersections of the sphere with a 2-plane. Thus we end up with a family of circles. In particular the topology of the resulting surfaces will be different than in the Euclidean or the hyperbolic case. Depending on the rotation speed, we end up in basically 3 situations:
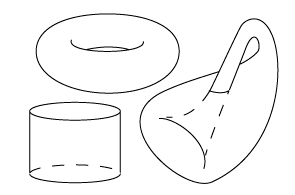
We get
- a cylinder: the speed is such that we never end up with the same circle going round the axis,
- a torus: after we traveled around the axis finitely often we end up up with the circle we started with and the surface closes up to an orientable surface, or
- a Klein bottle: here the surface also closes up, but the resulting surface is non-orientable.
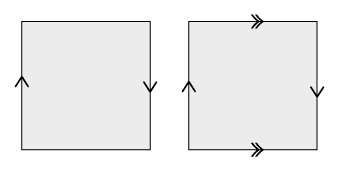
What is a Klein bottle? Maybe we first look at a quite famous example of a non-orientable surface – the Möbius strip.

It is the surface obtained by gluing a rectangular strip together along two opposite sides but with a twist of 180 degree.
If the surface is smooth one possible description of non-orientability is that the surface has no non-vanishing normal vector field. Thus one cannot distinguish the sides of the surface. So to speak non-orientable surfaces have only one side. This can be easily played through on the Möbius strip – walking once around a non-contractible loop one comes back upside down.
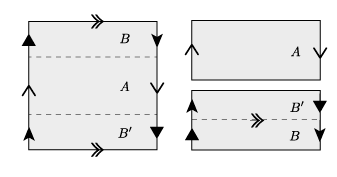
The Klein bottle is then obtained by gluing in addition the other two sides of the rectangle. Here a schematic picture of the Möbius band (left) and the Klein bottle (right) – the arrows indicate how to glue.
On the other hand a Klein bottle can be cut it into two Möbius strips. The picture below indicates how this can be done.
It is known that the stereographic projection of a minimal surface in \(\mathrm S^3\) is a Willmore surface. This we will use later to obtain a particularly nice Möbius strip from such a minimal Klein bottle.
So let us start with the construction of our minimal surfaces. First, like in hyperbolic space we can normalize the axis to be \(t\mapsto \gamma(t)=(\cos t,\sin t,0,0)\) – any great circle can be mapped to this curve by an isometry of \(\mathrm S^3\) (basically a rotation in \(\mathbb R^4\)). A unit length normal vector field to the axis is then certainly of the form \(t\mapsto (0,0,\cos g(t),\sin g(t))\), where \(g\) is some real-valued function. Since \(\Vert\gamma^\prime\Vert = 1\) we move along the axis with constant unit speed. Thus, up to isometry, a normal vector field \(N\) which rotates with constant speed \(\tau\in \mathbb R\) is given by \(N(t)=(0,0,\cos(\tau t),\sin(\tau t))\). The axis \(\gamma\) and the normal vector field \(N\) then let to the following easy formula for the immersion:\[f_\tau(x,y):= \cos y\, \gamma(x) + \sin y\, N(x) = \bigr(\cos y \cos x, \cos y \sin x, \sin y \cos (\tau x),\sin y \sin(\tau x)\bigr).\]
From the formula we can directly read of when this closes up – namely if and only if \(\tau = \frac{m}{n}\in \mathbb Q\). Actually these surfaces were studied by Lawson. A list of properties is given in Theorem 3 (page 351) in Lawson’s article ‘Complete minimal surfaces in \(\mathrm S^3\)’.
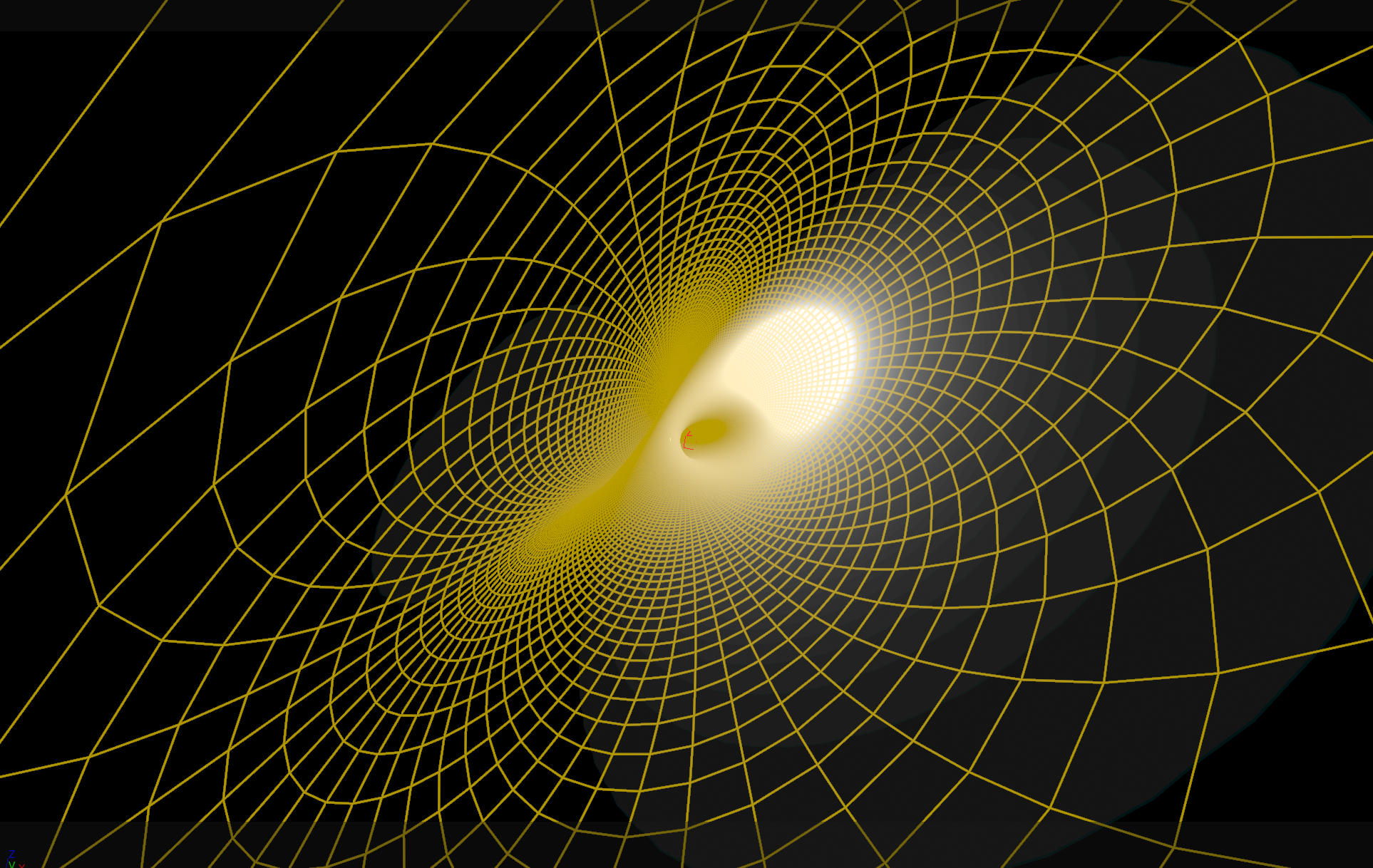
Given the formula, the surfaces are easy to implement. The last thing we have to do is to project it from \(\mathrm S^3\) into \(\mathbb R^3\). As we know this can be done by stereographic projection, usually from the north pole:\[\sigma\colon \mathrm S^3 \setminus \{(0,0,0,1)\} \to \mathbb R^3,\quad (x,y,z,w) \mapsto\Bigl(\frac{x}{1-w},\frac{y}{1-w},\frac{z}{1-w}\Bigr).\]Thus, at least as long as the surface does not go through the north pole, we can project the surface into Euclidean 3-space. Unfortunately, the surfaces pass through the north pole by construction. A screenshot of the result below.
Though this is easily fixed by choosing another point to project from or, alternatively, by applying a suitable rotation to \(\mathrm S^3\) before we project it by the stereographic projection \(\sigma\). E.g. if we multiply the sphere first with \(q = (1 + \mathbf i+ \mathbf j + \mathbf k)/2\), we find that the surface in fact looks quite nice – it is the Clifford torus (here \(\tau = 1\)).

For general \(\tau\) we get self-intersections and the surface hides what is going on ‘inside’. Below a picture for \(\tau=2\).

Again it is helpful to restrict the domain of definition of \(f_\tau\) and render just a part of the surface. Below we restricted \(f_\tau\) to the domain \([0,2\pi]\times[-\pi/4,\pi/4]\). Here the result for the surface above.

If we instead use \(\tau = 1/2\) we get a Möbius strip.

Extending the domain to \([0,2\pi]\times[-\pi/2,\pi/2]\) then yields a particularly nice Möbius strip – the so called Sudanese Möbius band – which is shown in the picture below. It is an embedded Willmore surface whose boundary curve is actually a round circle.

Homework (due 2 June): Write a network that visualizes the surfaces \(f_\tau\) in \(\mathbb R^3\). Build in parameters to change the resolution, the domain and the rotation speed \(\tau\). Finally render your own Sudanese surface.
