Let $\Sigma = (V,E,F)$ be a triangulated surface (with boundary). A realization of the surface in $\mathbb{R}^3$ is given by a map $p:V \rightarrow \mathbb{R}^3$ such that $p_i,p_j,p_k$ form a non degenerated triangle in $\mathbb{R}^3$ for all $\{i,j,k\} \in \Sigma$, (i.e. $p_i,p_j,p_k$ do not lie on a line). Some problems, like the plateau problem do not depend on the position of the vertices in the space, but only on the length of the edges:
\[l_{ij} = l_{ji} = |e_{ji}| \quad \quad {i,j} \in E. \]
If we have a realization of the surface in $\mathbb{R}^3$ there holds: $l_{ij}= l_{ji}=|p_i-p_j|$ and the edge length’s satisfy the triangle inequalities:
\[\mbox{For } \{i,j,k\} \in F \Rightarrow \left\{ \begin{matrix} l_{ij} < l_{jk} + l_{ki}, \\ l_{ki} < l_{ij} + l_{jk}, \\ l_{jk} < l_{ki} + l_{ij}. \end{matrix} \right .\]
Definition: A metric on a triangulated surface assigns a length to each oriented edge such that the triangle inequalities are satisfied.
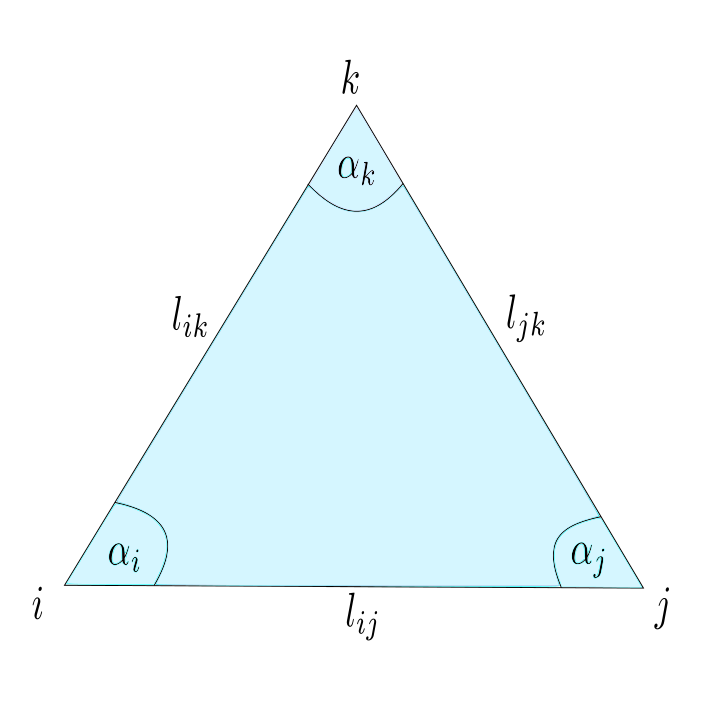 Note that every realization $p:V \rightarrow \mathbb{R}^3$ induces a metric on the underlying triangulated surface. On the other hand a triangulated surface with metric has several realization in $\mathbb{R}^3$, such that the metrics coincide. On a triangulated surface with metric every triangle has the structure of an euclidean triangle in $\mathbb{R}^2$, that allows us to interpolate $f:V\rightarrow \mathbb{R}$ to a piecewise affine function $\tilde{f}: C\left( \Sigma\right) \rightarrow \mathbb{R}$ and define the Dirichlet energy $E_D(f)$ as in the last lectures.
Note that every realization $p:V \rightarrow \mathbb{R}^3$ induces a metric on the underlying triangulated surface. On the other hand a triangulated surface with metric has several realization in $\mathbb{R}^3$, such that the metrics coincide. On a triangulated surface with metric every triangle has the structure of an euclidean triangle in $\mathbb{R}^2$, that allows us to interpolate $f:V\rightarrow \mathbb{R}$ to a piecewise affine function $\tilde{f}: C\left( \Sigma\right) \rightarrow \mathbb{R}$ and define the Dirichlet energy $E_D(f)$ as in the last lectures.
In particular, we can define angles and area using the cosine theorem:
\[\cos(\alpha_i) = \frac{l_{jk}^2-l_{ji}^2-l_{ki}^2}{2l_{ki}l_{ij}}\]
By the triangle inequalities we obtain that $0 < \gamma <\pi$ and the angles are well defined. With $\sin(\alpha_i) = \sqrt{1-\cos(\alpha_i)^2}$ we can define the cotangents weights and the area of the triangle $\sigma = \{i,j,k\}$ :
\[A_{\sigma} = \frac{1}{2} \sin{(\alpha_i})l_{ij} l_{ki}.\]
For a realization $p$ of $\Sigma$ with vertex positions $p_i,p_j,p_k$ and edges $e_{ij} = p_j-p_i, \ldots $ we obtain for $\sigma = \{i,j,k\} \in F$:
\[A_{\sigma}(p) = \frac{1}{2}\left| (p_j-p_i) \times (p_k-p_i) \right| = \frac{1}{2}\left| e_{ij} \times e_{ik}\right| = \frac{1}{2} \sin{(\alpha_i})\underbrace{|e_{ij}|}_{ =l_{ij}} \underbrace{|e_{ki}|}_{=l_{ki}},\]
and the total area is give by:
\[A (p) = \sum_{\sigma \in F} A_{\sigma}(p).\]
Definition: The following problem is the Plateau problem: Let $\Sigma$ be a triangulated surface with boundary and $q: V^{\partial} \rightarrow \mathbb{R}^3 $ a prescribed function. We are looking for a realization $p:V \rightarrow \mathbb{R}^3$ of $\Sigma$ such that:
1. $\left. p \right|_{V^{\partial}} = q,$
2. $ p$ has the smallest area among all realizations $ \tilde{p}$ of $\Sigma$, with $ \left. \tilde{p} \right|_{V^{\partial}} = q$.
In order to be able to solve the Plateau problem we have to consider variations of $p$:
Definition: A variation of $p$ with constant boundary assigns to each vertex $i \in V$ a curve $ t \mapsto p_i(t), $ $ t \in (- \epsilon ,\epsilon) ,$ such that:
1. $p_i(0) = p_i $ for all $i \in V.$
2. $p_j(t) = q_j $ for all $ t \in (- \epsilon ,\epsilon)$ if $j \in V^{\partial}$.
Definition: $p$ is called a minimal surface if it is a critical point of the area functional, i.e. :
\[\left. \frac{\partial}{\partial t} \right|_{t=0} A \left(p(t) \right) = 0,\]
for all variations of $p$ with constant boundary.
Lemma: $p$ is a minimal surface if and only if For each $i \in \overset{\circ}{V}$ and each curve $ t \mapsto p_i(t), $ $ t \in (- \epsilon ,\epsilon) $ we have:
\[\left. \frac{\partial}{\partial t} \right|_{t=0} A \left(p_i(t) \right) = \left. \frac{\partial}{\partial t} \right|_{t=0} \sum_{\sigma \in F \, \vert \, i \in \sigma} A_{\sigma} \left(p_i(t) \right) = 0.\]
I.e. $p$ is a critical point of the area functional with respect to all variations with constant boundary, if and only if it is a critical point for all those variations that only move one interior vertex.
Proof: $”\Rightarrow”:$ clear.
$”\Leftarrow:”$ Similar to the following fact from analysis:
All directional derivatives of a function $f: U \rightarrow \mathbb{R}, \quad U \subset \mathbb{R}^n$ vanish at $p \in U$ if and only if all partial derivatives of $f$ vanish at $p$.
$\square$
Theorem: $p$ is a minimal surface if and only if all tree components of $p$ are discrete harmonic functions with respect to the metric induced on $\Sigma$ by $p$.
Proof: 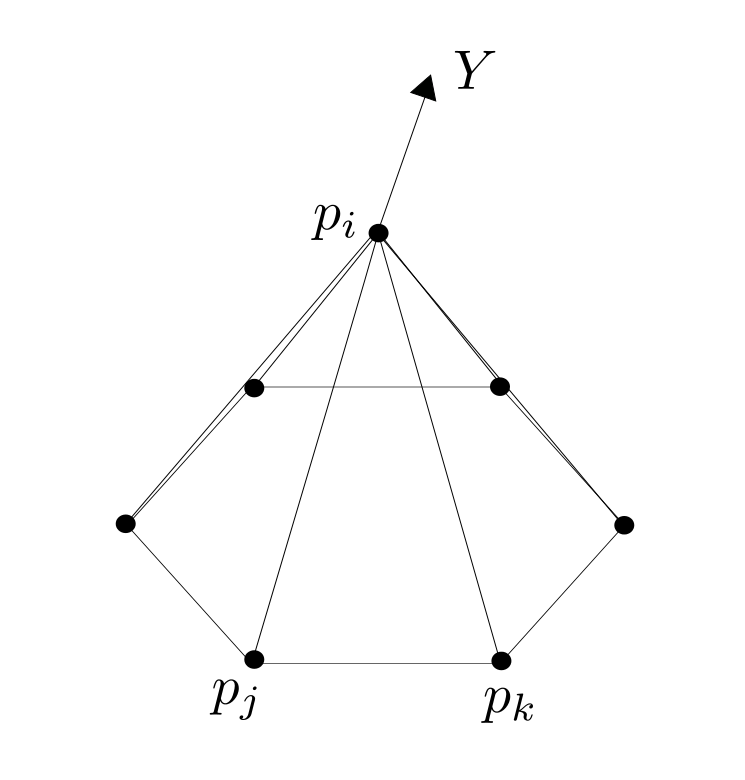 Fix $i \in \overset{\circ}{V}$ and let $ t \mapsto p_i(t), $ $ t \in (- \epsilon ,\epsilon) $ be a variation, that only moves $p_i$ and $Y:= p_i'(o). $ Further we define $\hat{F} := \left\{ \{i,j,k\} \in F \big \vert \mbox{ positive oriented} \right\}$ to be the set of positive oriented triangles that contain the vertex $i$. We have to show that there holds:
Fix $i \in \overset{\circ}{V}$ and let $ t \mapsto p_i(t), $ $ t \in (- \epsilon ,\epsilon) $ be a variation, that only moves $p_i$ and $Y:= p_i'(o). $ Further we define $\hat{F} := \left\{ \{i,j,k\} \in F \big \vert \mbox{ positive oriented} \right\}$ to be the set of positive oriented triangles that contain the vertex $i$. We have to show that there holds:
\begin{align}0=\left. \frac{\partial}{\partial t} \right|_{t=0} A \left(p_i(t) \right) &= \left. \frac{\partial}{\partial t} \right|_{t=0} \sum_{\{i,j,k\} \in \hat{F}} \left| (p_j-p_i(t)) \times (p_k-p_i(t))\right| \\&= \left. \frac{\partial}{\partial t} \right|_{t=0} \sum_{\{i,j,k\} \in \hat{F}} \left| e_{ij}(t) \times e_{ik}(t) \right|.\end{align}
Before we start with the proof remember these identities from analysis$\backslash$linear algebra
1. For a function $t\rightarrow v(t) \in \mathbb{R}^3$ there holds:
\begin{align} |v|’=\frac{\langle v, v’ \rangle}{|v|} \end{align}
2. For $a,b,c,d \in \mathbb{R}^3$ we have:
\begin{align} \langle a\times b, c \times d \rangle = \det \left( \begin{matrix} \langle a,c \rangle & \langle a,d \rangle \\ \langle b,c \rangle\ &\langle b,d \rangle\ \end{matrix} \right) = \langle a,c \rangle\langle b,d \rangle-\langle a,d \rangle\langle b,c \rangle.\end{align}
With $e_{i,j} = p_j-p_i$ we get $\dot{e_{ij}}=-Y$ and can compute now the variation of the area functional:
\begin{align*} \left. \frac{\partial}{\partial t} \right|_{t=0} &A \left(p_i(t) \right) = \frac{1}{2} \sum_{\{i,j,k\} \in \hat{F}} \frac{\langle e_{ij} \times e_{ik} , -Y \times e_{ik} – e_{ij} \times Y \rangle}{|e_{ij} \times e_{jk}|} \\ &= \sum_{\{i,j,k\} \in \hat{F}} \frac{-\langle e_{ij} ,Y\rangle |e_{ik}|^2 + \langle e_{ik},Y\rangle \langle e_{ij},e_{ik} \rangle -\langle e_{ik} ,Y\rangle |e_{ij}|^2 + \langle e_{ij},Y\rangle \langle e_{ij},e_{ik} \rangle}{2|e_{ij} \times e_{jk}|} \\ &= \bigl\langle Y ,\sum_{\{i,j,k\} \in \hat{F}} \frac{-e_{ij}|e_{ik}|^2-e_{ik}|e_{ij}|^2 + \langle e_{ij},e_{ik} \rangle (e_{ij} + e_{ik})}{2|e_{ij} \times e_{jk}|}\bigr\rangle \\&= \bigl\langle Y ,\sum_{\{i,j,k\} \in \hat{F}} \frac{\left( -\langle e_{ik},e_{ik} \rangle + \langle e_{ij},e_{ik} \rangle\right) e_{ij}+\left( -\langle e_{ij},e_{ij} \rangle + \langle e_{ij},e_{ik} \rangle\right) e_{ik}}{2|e_{ij} \times e_{jk}|} \bigr\rangle.\end{align*}
With \[-\langle e_{ik},e_{ik} \rangle + \langle e_{ij},e_{ik} \rangle = \langle e_{ik},e_{ij} -e_{ik}\rangle =\langle e_{ik},e_{kj} \rangle, \]
and
\[-\langle e_{ij},e_{ij} \rangle + \langle e_{ij},e_{ik} \rangle = \langle e_{ij},e_{ik} -e_{ij}\rangle = \langle e_{ij},e_{jk} \rangle,\]
We have:
\[ \left. \frac{\partial}{\partial t} \right|_{t=0} A \left(p_i(t) \right) = \bigl\langle Y ,\sum_{\{i,j,k\} \in \hat{F}} \left( \frac{ \langle e_{ik},e_{kj} \rangle e_{ij}}{2|e_{ij} \times e_{jk}|} \right) + \sum_{\{i,j,k\} \in \hat{F}} \left( \frac{\langle e_{ij},e_{jk} \rangle e_{ik}}{2|e_{ij} \times e_{jk}|} \right) \bigr\rangle. \]
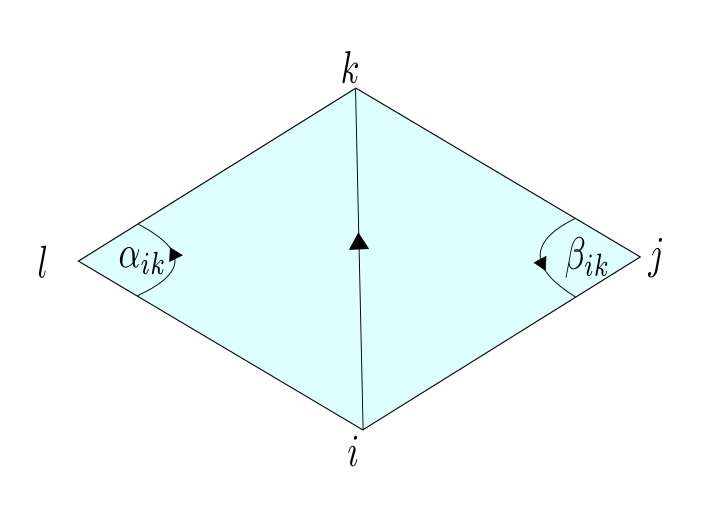
In an earlier lecture we showed that: $\cot(\beta_{ik}) = \frac{\langle -e_{ij},e_{jk}\rangle }{|e_{ij} \times e_{jk}|} $ and $ \cot(\alpha_{ik}) = \frac{\langle e_{il},e_{kl}\rangle }{|e_{ik} \times e_{il}|}. $
With an index shift in the first sum $(i,j,k) \rightarrow (i,k,l)$ we have now : \begin{align*} \left. \frac{\partial}{\partial t} \right|_{t=0} A \left(p_i(t) \right) & = \bigl\langle Y ,-\sum_{\{i,j,k\} \in \hat{F}} \frac{1}{2}\bigl( \cot(\beta_{ik}) + \cot(\alpha_{ik}) \bigr) e_{ik} \bigr\rangle \\ & = \bigl\langle Y , -\sum_{\{i,k\} \in \hat{E}} \frac{1}{2} \bigl( \cot(\beta_{ik}) + \cot(\alpha_{ik}) \bigr) (p_k – p_i) \bigr\rangle. \end{align*}
Since this has to hold for all variations $Y$ of $p_i$ and for all $i \in \overset{\circ}{V} $we finally get:
\[ \left. \frac{\partial}{\partial t} \right|_{t=0} A \left(p(t) \right) =0 \Leftrightarrow \sum_{\{i,k\} \in \hat{E}} \frac{1}{2} \bigl( \cot(\beta_{ik}) + \cot(\alpha_{ik}) \bigr) (p_k – p_i)=0 \quad \forall i \in \overset{\circ}{V}. \]
This means $p$ is an minimal surface if and only if all components of $p$ are harmonic with respect to the metric on $\Sigma$ induced by $p$.
$\square$
