In the lecture we have defined what we mean by a discrete minimal surface. The goal of this tutorial is to visualize such minimal surfaces.
Let \(\mathrm M\) be a discrete surface with boundary and let \(V, E, F\) denote the set of vertices, (unoriented) edges and faces. Once we have a discrete metric, i.e. a map \(\ell \colon E \to (0,\infty)\) such that the triangle inequalities hold,\[\ell_{ij} \leq \ell_{ik}+ \ell_{kj}, \quad \ell_{jk}\leq \ell_{ji} + \ell_{ik},\quad \ell_{ki} \leq \ell_{kj}+ \ell_{ji},\quad \textit{ for each }\sigma = \{i,j,k\},\]we can define the corresponding discrete Dirichlet energy \(E_D^\ell\):\[E_D^\ell (f) = \sum_{ij\in \tilde E} \omega_{ij}^\ell\,(f_j-f_i)^2,\quad \omega^\ell_{ij} = \tfrac{1}{2}(\cot \alpha_{ij} + \cot\beta_{ij}).\]Here \(\tilde E\) denote the positively oriented edges. Certainly the angles and thus the cotangent weights depend on the metric \(\ell\).
In particular, each map \(f\colon \mathrm M \to \mathbb R^3\), which maps thecombinatoric triangles to a non-degenerate triangles in \(\mathbb R^3\), yields an induced discrete metric,\[\ell_{ij} = |p_j – p_i|.\]We have seen in the lecture that a surface is minimal, i.e. a critical point of the area functional under all variations fixing the boundary, if and only if it solves the Dirichlet problem (with respect to its induced metric): For each interior vertex \(i\in\mathring V\) we have\[-\tfrac{1}{2}\sum_{\{i,j\}\in E}\,\omega_{ij}^\ell f_i +\tfrac{1}{2}\sum_{\{i,j\}\in E}\,\omega_{ij}^\ell f_j = 0,\]where \(\ell\) denotes the metric induced by \(f\).
Unfortunately, unlike the Dirichlet problem, this is a non-linear problem – the cotangent weights depend on \(\ell\) in a complicated way. Though, fortunately, we can solve it in many cases by iteratively solving a Dirichlet problem (here a paper that describes this). Since we know how to solve the Dirichlet problem we can implement this method without any effort.
The network above visualizes Plateau’s problem: Given a space curve \(\gamma\) compute a minimal disk with boundary \(\gamma\). Actually this corresponds to a soap film spanned into a wire.

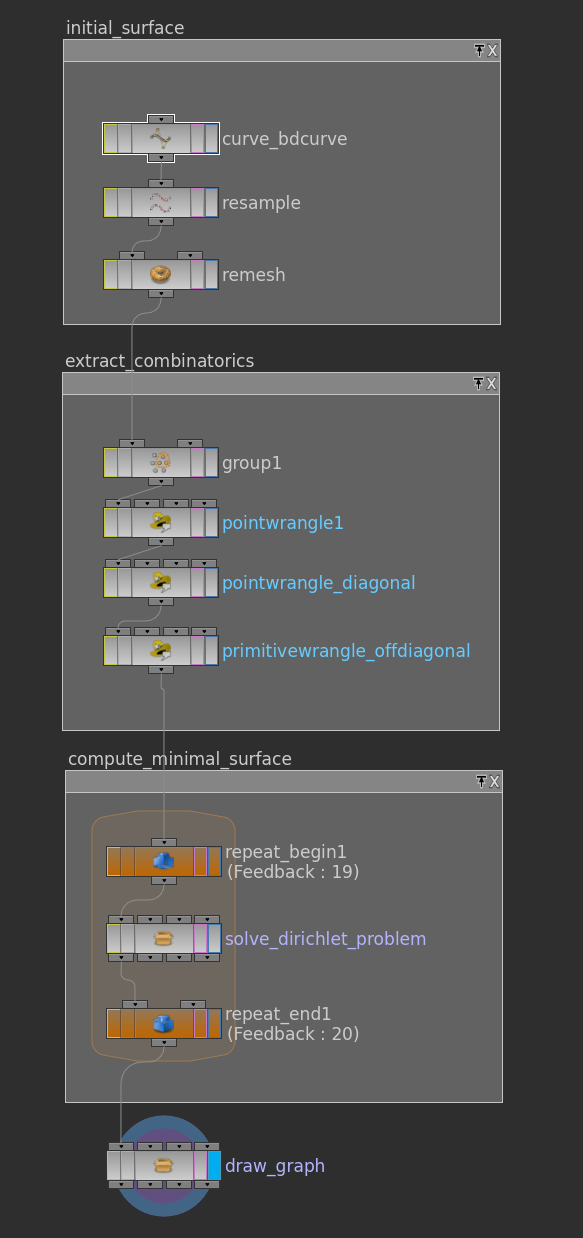
In the discrete setup we start with some discrete space, say generated by a curve node (probably followed by a resample node), which we then stick into a remesh node to get a reasonably triangulated disk spanned in. Then we can apply the iteration to this input. Below one possible result:

For rendering we used here the following texture in the mantra surface material. To generate texture coordinates one can use the nodes uvunwrap or uvtexture.
The algorithm is not restricted to disks. We can stick in any surface we want. Another nice example is e.g. obtained by starting with a cylinder of revolution. Here the minimal surface becomes a part of a catenoid or, if the cylinder’s height becomes to large, it degenerates to a pair of flat disks (connected by a straight line). In the picture below the last two circles are already too far apart – the surface starts to splits into two parts.

As a last example we can start with the unit sphere into which we cut several holes. If we want nice symmetries we could use a platonic solid node to copy smaller spheres to the vertex positions of e.g. an octahedron. The area enclosed by the smaller spheres we then subtract from the unit sphere with help of a cookie node. If we run then the algorithm on this input we end up with nice symmetric minimal surface. For a certain radius of the holes the surface is close to the Schwarz P surface.

Again one can observe the same effect as for the cylinder – if the holes get to small the minimal surface degenerates to several spheres connected to the origin.
Homework (due 12/14 July). Build a network that computes from a given discrete surface with boundary a minimal surface with the same boundary. Use this network to solve Plateau’s problem and to compute symmetric minimal surface from a sphere with holes as described above.
