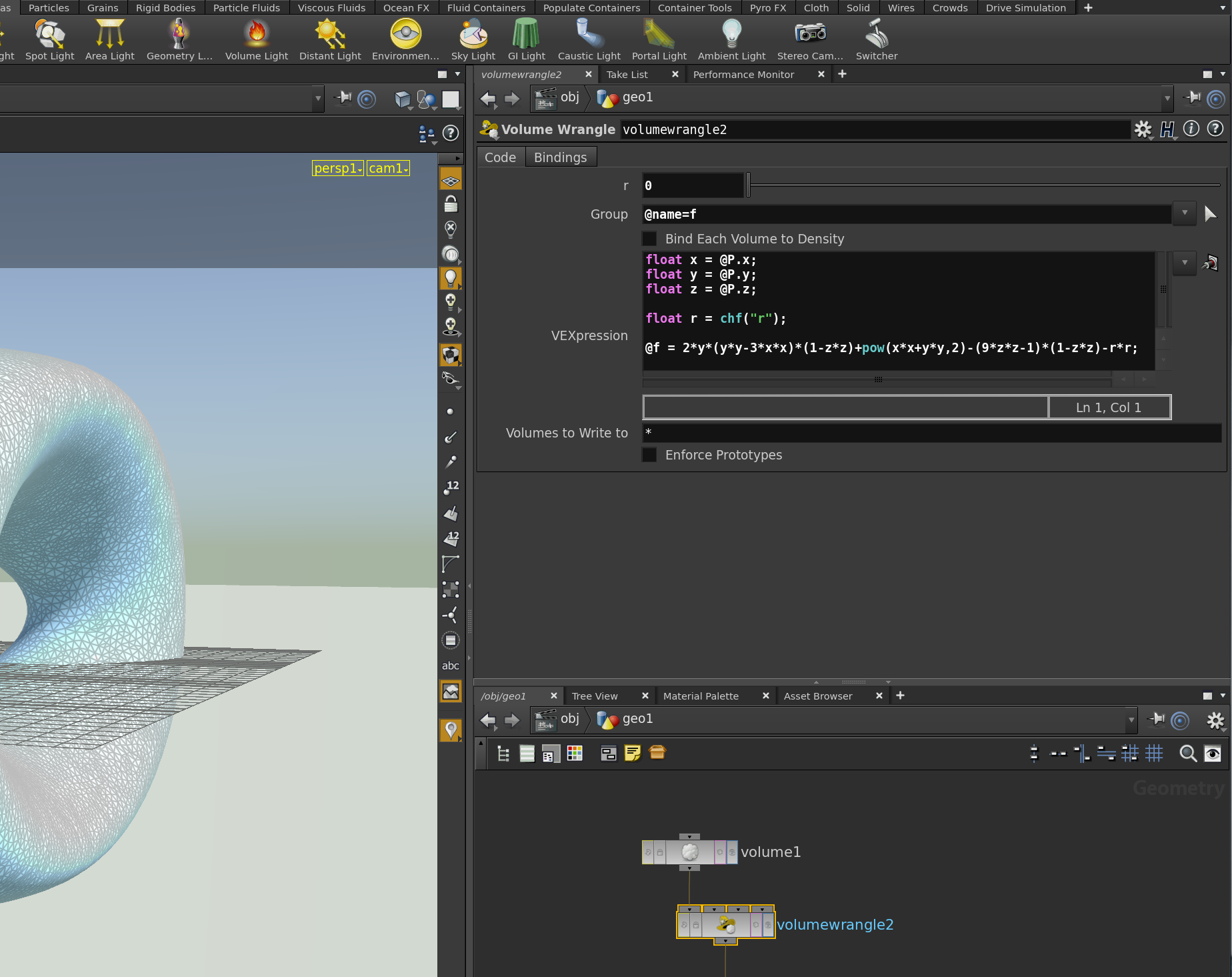
Quaternions, $\mathbb{H}$ are a number system like real or complex numbers but with 4 dimensions. In particular, $\mathbb{H}$ is nothing but $\mathbb{R}^4$ together with a multiplication law. The identification of $\mathbb{H}$ and $\mathbb{R}^4$ is given by:
$$ \mathbb{H} = \lbrace x_0 + x_1 {\bf i} + x_2 {\bf j} + x_3 {\bf k} \,\vert \,x_0,x_1,x_2,x_3 \in \mathbb{R} \rbrace.$$
With the usual addition and scalar multiplication inherited from $\mathbb{R}^4$, $\mathbb{H}$ becomes a four dimensional $\mathbb{R}$ vector space with canonical basis $\{ 1, {\bf i}, {\bf j}, {\bf k} \}.$ The quaternion multiplication is defined by:
\begin{align*}
&\left(x_0 + x_1 {\bf i} + x_2{\bf j} + x_3 {\bf k} \right) \cdot \left(y_0 + y_1{\bf i} + y_2{\bf j} + y_3 {\bf k} \right) \\:= & \left(x_0 y_0 – x_1 y_1 – x_2 y_2 – x_3 y_3 \right) \\
+ & \left(x_0 y_1 + x_1 y_0 + x_2 y_3 – x_3 y_2 \right){\bf i} \\
+ & \left(x_0 y_2 – x_1 y_3 + x_2 y_0 + x_3 y_1 \right){\bf j} \\
+ & \left(x_0 y_3 + x_1 y_2 – x_2 y_1 + x_3 y_0 \right) {\bf k}.
\end{align*}
A more simple way to define the quaternion multiplication is to say that the multiplication with $\alpha \in \mathbb{R}$ works as usually and that ${\bf i}, {\bf j}, {\bf k}$ satisfy the following multiplication rules:
\[{\bf i}^2 = {\bf j}^2 = {\bf k}^2 = -1,\quad {\bf ij}=-{\bf ji}={\bf k}, \quad {\bf jk}=-{\bf kj}={\bf i}, \quad {\bf ki}=-{\bf ik}={\bf j}.\]
${\rm Re}(\mathbb{H}) := span\{1\}$ is called the real part of $\mathbb{H}$ and ${\rm Im}(\mathbb{H}) := span\{{\bf i}, {\bf j}, {\bf k}\}$ the imaginary part and there holds: $\mathbb{H} = {\rm Re}(\mathbb{H}) \oplus {\rm Im}(\mathbb{H})$. If we identify ${\rm Re}(\mathbb{H})$ with $\mathbb{R}$ and ${\rm Im}(\mathbb{H})$ with $\mathbb{R}^3$, we can write any ${\bf x} \in \mathbb{H} $ as: $\quad {\bf x} = \alpha + {\bf v},\quad $ for some $\alpha \in \mathbb{R}$ and ${\bf v}\in \mathbb{R}^3.$ This notation gives us a new expression of the quaternion multiplication using the scalar and cross product of $\mathbb{R}^3$:
$${\bf p}{\bf q} = (\alpha + {\bf v}) (\beta + {\bf w}) = \alpha \beta -\langle {\bf v},{\bf w}\rangle + \alpha {\bf w}+ \beta {\bf v} + {\bf v} \times {\bf w}.$$
Due to the fact that the cross product is skew symmetric, we immediately see that the quaternion multiplication is not commutative, i.e. in general there holds ${\bf p}{\bf q} \neq {\bf q}{\bf p}$.
Proposition: The quaternion multiplication is associative i.e. for ${\bf p}, {\bf q}, {\bf r} \in \mathbb{H}$ there holds:
$$ ({\bf p}{\bf q}){\bf r}={\bf p}({\bf q}{\bf r})$$
Proof: Let \[ I := \left(\begin{array}{cc} 1 & 0 \\0 & 1\end{array} \right), \quad X := \left(\begin{array}{cc}{\bf i} & 0 \\ 0 & -{\bf i}\end{array}\right), \quad Y := \left(\begin{array}{cc} 0 & -1 \\ 1 & 0\end{array}\right), \quad Z := \left(\begin{array}{cc} 0 & -{\bf i} \\- {\bf i} & 0\end{array}\right). \]
Now we can define a linear map \begin{align*} F:\mathbb{H} &\rightarrow \mathbb{C}^{2\times 2} \\ x_0 + x_1 {\bf i} + x_2 {\bf j} + x_3 {\bf k} &\mapsto x_0 I + x_1 X + x_2 Y + x_3 Z \end{align*}
A straight forward calculation shows that $I,X,Y,Z$ satisfy the following product rules with respect to the matrix multiplication:
\begin{align*} I^2=I , \quad &IX=XI=I, \quad XY=-YX = Z, \\ &IY=YI =Y , \quad YZ=-ZY=X, \\ &IZ=ZI=Z, \quad ZX=-XZ =Y.\end{align*}
Therfore, $F$ is an algebra isomorphism onto its image. Due to the fact that the matrix multiplication is associative we obtain that the quaternion multiplication is associative too.
The conjugate of an quaternion number $ {\bf x} = \alpha + {\bf v}$ is given by $ {\bf\bar{ x}} = \alpha – {\bf v}$.
Proposition: For $ {\bf p}, {\bf q} \in \mathbb{H}$ there holds : $ {\bf\overline{ pq}} = {\bf\bar{ q}}{\bf\bar{ p}}.$
Proof: \begin{align*} {\bf p}{\bf q} &= \alpha \beta -\langle {\bf v},{\bf w}\rangle + \alpha {\bf w}+ \beta {\bf v} + {\bf v} \times {\bf w} \\
\overline{ {\bf p}{\bf q}} &= \alpha \beta – \langle {\bf v},{\bf w}\rangle – \alpha {\bf w} – \beta {\bf v} + {\bf w} \times {\bf v}\\
&= {\bf \bar{q}}{\bf \bar{p}}\end{align*}
$\mathbb{H}$ also inherits the euclidean norm from $\mathbb{R}^4$: $|{\bf p}| = (\sum_{i=0}^3 p_i^2)^{\frac{1}{2}}$. Similar to the complex numbers we have $|{\bf p}|^2 = {\bf p}{\bf \bar{p}}={\bf \bar{p}}{\bf p}$. Additionally, there holds the following useful formula:
Proposition: For ${\bf p},{\bf q} \in \mathbb{H}$ there holds: $|{\bf p}{\bf q}|=|{\bf p}||{\bf q}|.$
Proof:\begin{align*} |{\bf p}{\bf q}| =(({\bf p}{\bf q}) (\overline{{\bf p}{\bf q}}))^{\frac{1}{2}} = ({\bf p}{\bf q} {\bf \bar{q}}{\bf \bar{p}})^{\frac{1}{2}} = ({\bf p} |{\bf q}|^2{\bf \bar{p}})^{\frac{1}{2} } = (|{\bf p}|^2 |{\bf q}|^2)^{\frac{1}{2} } = |{\bf p}||{\bf q}|. \end{align*}
Note that for ${\bf q} \in \mathbb{H}$ the inverse element with respect to the quaternion multiplication is given by
$${\bf q} ^{-1} = \frac{{\bf \bar{q}} }{|{\bf q}|^2 }.$$
For quaternions with unit length this gives us immediately ${\bf q} ^{-1} = {\bf \bar{q}}.$
What makes quaternions so useful is the fact that one can describe rotation in $\mathbb{R}^3$ with them in a very elegant way. Therefore, we have to consider $\mathbb{R}^3$ as ${\rm Im}(\mathbb{H})$.
Theorem: Let ${\bf a} \in \mathbb{R}^3$ with $|{\bf a}|=1$ , $\alpha \in \mathbb{R}$ and ${\bf q} = \cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a}$. Then for all ${\bf y} \in \mathbb{R}^3$ we have:
(i) ${\bf q}{\bf y} {\bf \bar{q}} \in {\rm Im} (\mathbb{H}) = \mathbb{R}^3$
(ii) The map $F:\mathbb{R}^3 \rightarrow \mathbb{R}^3$, ${\bf y} \mapsto {\bf q}{\bf y}{\bf \bar{q}}$ is a rotation around ${\bf a}$ by the angle $\alpha$.
Proof: (i) First note that a quaternion ${\bf y}$ is purely imaginary if and only if ${\bf \bar{y}}= -{\bf y}$. Thus we have to show $\overline{{\bf q}{\bf y}{\bf \bar{q}}}= \,- {\bf q}{\bf y}{\bf \bar{q}}$.
$$\overline{{\bf q}{\bf y}{\bf \bar{q}}} = {\bf q}{\bf \bar{y}}{\bf \bar{q}} = \,- {\bf q}{\bf y}{\bf \bar{q}}.$$
(ii) $F$ is a linear map and therefore completely determined by its action on a basis. We extend ${\bf a}$ to an positive oriented orthonormal basis $\{{\bf a}, {\bf b}, {\bf c} \}$ of $\mathbb{R}^3$.
\begin{align*}F({\bf a}) = {\bf q}{\bf a}{\bf \bar{q}} &= \left( \cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a}\right) {\bf a}\left(\cos\left(\frac{\alpha}{2}\right) – \sin\left(\frac{\alpha}{2}\right) {\bf a}\right) \\ &= \left( \cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a}\right)\left(\cos\left(\frac{\alpha}{2}\right){\bf a} + \sin\left(\frac{\alpha}{2}\right)\right ) \\ &= \left( \cos^2\left(\frac{\alpha}{2}\right) + \sin^2\left(\frac{\alpha}{2}\right)\right) {\bf a} + \cos\left(\frac{\alpha}{2}\right) \sin\left(\frac{\alpha}{2}\right) (1+{\bf a}^2) \\ & = {\bf a}.\end{align*}
In the last step we used that ${\bf a}^2= \,-1$. This gives us that the ${\bf a}$-axis is invariant under $F$. Now we consider the action of $F$ on the plane orthogonal to ${\bf a}$, i.e. the plane spanned by $ {\bf b}$ and ${\bf c}$. Since $ \langle {\bf a}, {\bf b} \rangle =0 $ we have:
$$ {\bf a}{\bf b} = {\bf a} \times {\bf b} = \,- {\bf b} \times {\bf a} = \,- {\bf b}{\bf a}.$$
Using this and the addition formulas for cosine and sine we get:
\begin{align*} F({\bf b}) & = \left( \cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a}\right) {\bf b} \left(\cos\left(\frac{\alpha}{2}\right) – \sin\left(\frac{\alpha}{2}\right) {\bf a}\right) \\ &= \left( \cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a}\right) \left(\cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a}\right) {\bf b} \\ &=\left( \cos(\alpha) + \sin(\alpha) {\bf a}\right) {\bf b} = \cos(\alpha){\bf b} + \sin(\alpha)\left( {\bf a} \times {\bf b}\right) \\ &= \cos(\alpha){\bf b} + \sin(\alpha) {\bf c}\end{align*}
Analog we obtain $F({\bf c}) = \cos(\alpha){\bf b} – \sin(\alpha) {\bf b} $ and the matrix representation of $F$ with respect to the basis $\{{\bf a}, {\bf b}, {\bf c} \}$ is given by:
\[ F = \left(\begin{array}{ccc} 1 & 0 & 0 \\0 & \cos(\alpha) & -\sin(\alpha) \\ 0 & \sin(\alpha) & \cos(\alpha) \end{array} \right)\].
Now it is easy to see that $F$ describes a rotation around ${\bf a}$ by the angle $\alpha$.
Corollary: For every $ {\bf q} \in \mathbb{H}\backslash \{0\}$ the map $F:\mathbb{R}^3 \rightarrow \mathbb{R}^3$, ${\bf y} \mapsto {\bf q}{\bf y}{\bf q}^{-1}$ is a rotation.
Proof: With ${\bf q} ^{-1} = \frac{{\bf \bar{q}} }{|{\bf q}|^2 }$ we get:
$$ {\bf q}{\bf y}{\bf q}^{-1} = \frac{{\bf q}}{|{\bf q}|}{\bf y}\overline{\left(\frac{{\bf q} }{|{\bf q}| }\right)}$$
Since $\frac{{\bf q}}{|{\bf q}|}$ has unit length there exists ${\bf a} \in \mathbb{R}^3$ with $|{\bf a}|=1$ and $\alpha \in \mathbb{R}$ such that: $\frac{{\bf q}}{|{\bf q}|} = \cos\left(\frac{\alpha}{2}\right) + \sin\left(\frac{\alpha}{2}\right) {\bf a} $ and we can apply the theorem.
Note that the quaternion multiplication corresponds to the concatenation of rotations. Let ${\bf p}, {\bf q} \in \mathbb{H}$ with $|{\bf p}|= |{\bf q}| =1$ and $F,G:\mathbb{R}^3 \rightarrow \mathbb{R}^3$ the corresponding rotations i.e. $F({\bf y}) = {\bf q}{\bf y}{\bf \bar{q}}$ and $G({\bf y}) = {\bf p}{\bf y}{\bf \bar{p}}$, then we get for the concatenation:
$$\left( F \circ G\right) (y) = {\bf q}\left( {\bf p}{\bf y}{\bf \bar{p}} \right) {\bf \bar{q}} = \left({\bf q} {\bf p}\right){\bf y}\overline{\left({\bf q} {\bf p}\right)}.$$